Scheduling of agents in inbound multilingual call centers
Luiz Henrique Santanna Barbosa1, Carlos Francisco Simões Gomes1, Maria Cecilia C. Chaves2
1 Fluminense Federal University
2 Federal University of Rio de Janeiro
Abstract
This paper presents an Integer Linear Programming model, which enables the scheduling of agents in call centers according to segmentation by skills, as well as the inclusion of labor law restrictions. The results from the experimental application of this method to situations involving real-time problems are presented, wherein the necessary shifts to meet forecasted demand are provided, in addition to an economically optimum combination of agents and skills, generating a solution, which is sufficient to maintain the desired level of service at the lowest cost possible. The approach proposed in this study presents an alternative worthy of consideration, since it is able to successfully incorporate the flexibility of call centers with skills-based routing in an easy-to-implement model that has proven to be effective in experiments conducted in on-the-job settings. Advances in information technology and telecommunications in recent years have increasingly heightened the presence of call centers in the day-to-day of companies and their customers. Call center management should endeavor to achieve a balance between technical performance and economic performance (labour costs, equipment, trunks and rates). It is estimated that 70% of the operating costs of call centers are currently related to labor costs. This paper provides research on how to significantly reduce personnel-related operational costs without negatively affecting the quality of the service.
Keywords: Planning; Allocation; Call Centers; Scheduling; Skill-Based Routing; Integer Programming.
1 Introduction
In the last decade, call center operation centers have become an inevitable part of many global businesses (Aktekin, 2014). Many commercial enterprises and public agencies operate centralized call centers to provide effective inbound service as pointed out by Dietz (2011). Telephone call centers are a central component in different public and private organizations. Call Centers provide a communication channel between companies and their customers, and call center performance is very important to a company’s reputation (Dudin et al., 2013; Gong et al., 2015).
In recent decades, call centers have proliferated and grown in importance for companies. As economies grow, the focus of companies on relationships with their customers also grows, and call centers are one of the main tools used to achieve this (Dietz, 2011). This paper focuses on daily scheduling in which a real-time problem is addressed. The study was conducted in a medium-sized Brazilian call center, which provides customer service and receives calls in three different languages, where call agents must be able to speak in the respective language.
The objective of this study is to provide an integer-programming model that enables agents in inbound call centers to be scheduled based on segmentation by skills (practical in nature). The models also permits the inclusion of Brazilian labor law restrictions, as well as compliance with the service levels that call centers must adhere to, besides tapping into the advantages of segmenting call centers by skills, thereby optimizing the use of agents.
This paper proposes an alternative approach to resolve scheduling problems in call centers through the use of skill-based routing. This model must meet current demand and allow for future expansion, caused by increased call demand, as well as increased supply of operators.
After literature review on the subject, an integer-programming model was created to solve a problem in the labor management process of call centers. Numerical experiments were also conducted in a medium-sized Brazilian call center, which demonstrated the effectiveness of the approach proposed in this study and improved the scheduling of agents in the company that was examined. At the end of this article, a case study analysis will be presented.
The paper is organized as follows. Section 2 contains an overview of scheduling in multi-skill call centers, while Section 2.2 deals more specifically with formulas based on linear models to solve scheduling problems in call centers through the use of skill-based routing. Following this, we introduce our suggested approach to model the problem. The case study is then presented in Section 4 and the concluding remarks are made in Section 5.
2 Literature Review
Many organizations have recently come to rely on call centers as a major vehicle to serve their customers and support marketing efforts (Tjosvold et al., 2014).
A key aspect in managing them is the staffing and scheduling of agents (who answer the calls), which is made difficult, in particular, by the high uncertainty associated with the volume and time-distribution of inbound calls (Channouf et L’Ecouyer, 2012).
In Brazil, call centers operate primarily in the realm of Customer Service, Debt Collection and Telemarketing (Callcenterinf, 2012). As economies and, consequently, the volume of transactions of companies expand, it is to be expected that the level of interaction between companies and their customers will likewise increase. With a greater number of customers, companies must also be prepared to handle an increased volume of interaction with these customers, whether through providing customer support services to receive suggestions and complaints, or to supply information and support for its products and services (Rolfini, 2013).
This expectation of growth, prompted by a strong economy, leads companies to improve the quality of their products and services, as well as communication channels with their customers. Quality of service is one of the main concerns in call center management and is a determining factor of a company’s competitiveness. Therefore, providing an efficient channel of communication via a call center is not only an important asset to reach new customers, but also an essential requirement to retain current customers (Callcenterinf, 2012). Therefore, it is important that the customer’s experience when communicating with the company is not slow.
In 2008, the Call Center Law (Brazilian law), which regulates waiting time and quality standards for different services, went into effect (Barbosa, 2011). This law made it necessary for companies to pay more attention to the quality of services offered by phone, resulting in an increased number of customer service positions and further contributing to the growth of the sector. Therefore, in the wake of this law, the quality of services offered by phone has not only become a matter of competitiveness, but bears consequences that are more important.
Managing a call center is a diversified challenge due to many complex factors related to uncertain and time-varying demand for service (Gans et al., 2003; Legros, 2015). With proper planning, it is possible for call centers to achieve excellent service quality and high productivity, so that a few hundred agents are able to answer thousands of calls per hour, with little idle agent time and no customers receiving a busy signal. In order to attain this level of operational quality, the planning of these call centers must be done using quantitative approaches (Aktekin, 2014; Gans et al., 2003; Brown, 2005; Koole, 2013; 2012; Fiems, 2008; Jouini et al., 2009).
Call centers have grown in number and size (Aksin et Harker, 2003). The services they offer have also dramatically increased. Therefore, it is not possible for most call centers to create a structure in which all agents are capable of attending all types of calls (Dietz, 2011). As a result, generally, the phone system first captures information about the call in order to determine which agents can attend the call, and then it is transferred accordingly.
There is extensive and growing literature on call centers and, in general, on contact centers. See Aguir et al. (2008), Aksin et Harker (2003), Avramidis et al. (2010), Bhulai et al. (2008), Channouf et L'Ecuyer (2012), Dietz (2011), Dietz et Vaver (2006), Koole (2013), Robbins et Harrison (2010), Dudin et al. (2013), Legros, Jouini, Dallery (2011), Gong et al. (2015), Kim et Park (2010), Cezik et L’Ecuyer (2008). We consider Bhulai et al. (2008) to be the model that has most of the similarities with our problem and purpose.
In traditional call centers, agents are divided into several departments, where every department is responsible for one or more types of calls. Calls are then routed accordingly to the department responsible. Every department is fully independent and each call type can be resolved by each specific department (Reynolds, 2003). The agents are limited to a single department and are trained to answer and resolve specific calls pertaining to their area of responsibility within the department. In these call centers, operational planning is relatively simple. However, this strategy may often prove to be inefficient. Peak call hours often vary according to each different call type, and this may result in a considerable amount of leftover "idle time" for agents. Aside from this, due to the fact that departments are independent and limited to only answering specific call types, the size of each department is relatively small. It is as though each department were its own independent call center. However, if these departments were combined, the number of agents per department would be greater, resulting in cost reductions through economies of scale (Gans et al., 2003; Koole, 2013; 2012).
Modern call centers use skill-based routing (SBR). In such centers, agents are categorized according to their specific skills and calls are routed to any available agent who has the necessary skill to attend the call (Wallace et Whitt, 2005). This affords greater flexibility in dealing with variations in call volumes, helps even out the quality of service among the various call types and increases the number of available agents, thus minimizing staffing costs. However, skill-based routing considerably heightens the complexity of the operational planning process, because the more skills an agent has, the more it costs to hire them. The goal in implementing shift scheduling in multi-skill call centers is to find the right combination of agents and abilities (Koole, 2013).
2.1 Scheduling of Agents in Call Centers
There are different papers that address the issue of scheduling (Aksin et al., 2007; Sawik, 2010). Dantzig (1954) provides a scheduling model through integer programming which can be applied to simple call centers. Pinedo (2005) takes this model a step further by incorporating penalties for failure to comply with demand and for surplus agents. Thompson (1997), Atlason et al. (2004) and Koole (2013) present models where, besides a minimum level of service, there is also an additional level of service. However, they do not take into consideration the skills of agents.
Cordone et al. (2011) present a heuristic where the relaxation of an integer program is performed and the variables are manipulated iteratively until an integer result is achieved. The algorithm takes into account the skills of agents and incorporates rest breaks, in addition to balancing the types of employment contracts (full or part-time). However, the algorithm does not take into consideration different costs according to the skills of agents. Channouf et L'Ecuyer (2012) present an algorithm for multi-skill call center sizing through simulation and linear programming, without solving, however, the scheduling problem of Bhulai et al. (2008), who propose an algorithm for multi-skill scheduling in two stages: in the first, they use the model designed by Channouf et L'Ecuyer (2012) to determine the optimum number of agents per profile; in the second they use an integer program to solve the scheduling problem. The model proposed herein is the result of adaptations made to the work of Bhulai et al. (2008).
2.2 Multi-skill scheduling models
In Bhulai et al. (2008), an algorithm is presented that, in the first stage, calculates the necessary number of agents for each profile and, then, creates the shifts of these agents in order to meet the minimum demand calculated in the previous stage. Since the focus of this study is scheduling, only the second stage of the algorithm will be described and tested in this article, in order to have a basis of comparison. The aforementioned heuristic to reduce the number of possible work shifts will not be considered. In addition, the nomenclature and way of presenting the variables were modified to make the concepts used throughout this article homogeneous and to obtain a basis of comparison for the performance of the model proposed in this study.
Lastly, demand is calculated using the algorithm presented in Channouf et L'Ecuyer (2012), which uses simulation to determine the number of agents per profile needed for each time interval. In this paper, demand is measured according to call type and not agent profile, which made it necessary to adapt the formula described in Bhulai et al. (2008). As a result, the scheduling model uses the following adapted formula:
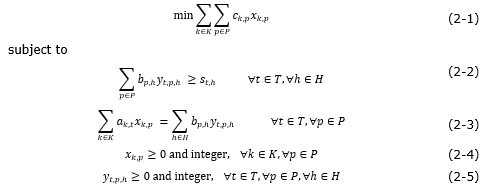
Where:
P: set of profiles of existing agents;
T: time intervals considered in the planning horizon;
H: set of existing skills;
K: set of possible shifts;
st,h: indicates the number of agents with skill h needed for time t;
ak,t: binary variable indicating whether an agent assigned to shift k works in period t.
The decision variables xk,p represents the number of agents with profile p in shift k. Finally, cost, which varies not only according to shift, but also to each agent’s profile, is represented by the matrix ck,p.
In this scheduling model, an allocation was made for each time interval to determine the number of agents that would be answering each call type. This allocation is expressed through the decision variable yt,p,h, where t is the time interval, p is the profile of the agent and h is the type of call (or skill) that the agent will be answering. The binary matrix bp,h is also introduced, which assigns 1 if the agent with profile p has skill h, or 0 if not.
Thus, for each time interval, the number of agents per profile is allocated to the type of call they would be answering during a certain time interval. The sole purpose of this allocation is to ensure that the number of agents used to meet the demand for each call type is consistent with the number of agents available, according to the specific shifts and profiles. This information is irrelevant for operational planning, since it is a decision made during runtime by the ACD. Therefore, the decision variables yt,p,h have no usefulness, except for ensuring data consistency. In Bhulai et al. (2008), it was reported that good runtimes were obtained from its formula, but that the number of variables grows rapidly when more call types, agent profiles or a larger planning horizon are added. With this in mind, efforts were made to simplify this model by reducing the number of variables and, consequently, runtime.
3 Model Formulation
The proposed model uses the same objective function (2-1) presented earlier. However, it uses another approach to guarantee that available agents, according to their skills, meet demand. This formula ensures that, for each subset of skills H, the sum of the demands for these skills is less than or equal to the number of agents available, i.e. those agents whose shifts determine that they will be working during the time interval and who have the ability to answer calls requiring at least one of these skills. For this purpose, we introduce the following function:

Lastly, the model is supplemented with restrictions that ensure that the demand for each call type is met.
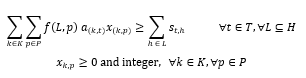
The matrix st,h , previously described in the model by Dietz (2011) and the formula based on Bhulai et al. (2008), is also used in this formula and indicates the demand for agents with skill h in time interval t.
The complete formula, therefore, is expressed by the objective function (2-1) and the restrictions (3-2) and (3-3):

Thus, a relatively simple model that is able to solve multi-skill scheduling problems in a very short computational time (seconds or fractions of a second) was obtained. Computational time will obviously depend on the number of shifts, which varies according to length of time of service and number of skills and skill sets.
3.1 Proof of Correctness of the Proposed Model
As previously noted, Bhulai et al. (2008) model scheduling problems in multi-skill call centers can be interpreted as minor network flow problems in each time interval. During each interval, available agents in each group are redistributed to meet the demand for each skill. However, for planning purposes, it can be said that allocating these groups of agents according to call type is irrelevant. When it comes to operational planning, what counts is that the results obtained ensure that the allocation is doable at the time of implementation.
Gans et al. [2003] demonstrate the following theorem that enables one to verify the feasibility of a network flow:
Theorem. A network flow problem will have a solution if, and only if, for any subset S of N, the sum of the demands of the nodes pertaining to S is less than the sum of the capacities of the arrows directed to the elements of S.
To illustrate this theorem and its application, a simple example (Figure 1) of a call center with two call types and three different profiles is shown below:
Figure 1. Network flow example of a call center with two skills and three agent profiles.
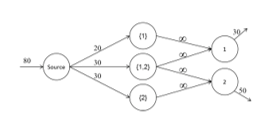
In this call center, profile {1} only has the ability to serve call type 1; profile {2} only has the ability to serve call type 2; profile {1, 2} has the ability to serve call types 1 and 2.
There is a demand for 30 agents with skill 1 and 50 agents with skill 2, as illustrated by the arrows stemming from the nodes representing skills. The arrows have a restriction as far as their capacity, as indicated by the number above each arrow. The arrows originating from the profile nodes, pointing to the nodes representing skills, have infinite capacity, whereas the arrows pointing toward the profile nodes have a maximum capacity restriction of 20, 30 and 30 for profiles {1}, {1, 2} and {2}, respectively.
By applying Gale’s (1957) theorem Gans et al. (2003) considers that it is possible to determine the feasibility of solving this problem. To this end, the subsets of N are selected to verify whether the sum of the demands of the selected elements will be less than, or equal to, the capacity of the incoming arrows. The subsets containing only nodes that represent skills are ignored, based on the fact that the incoming arrows have infinite capacity (Bertsimas et Xuan, 2010; Stolletz, 2003). Figure 2 illustrates the subsets S of the set N of nodes which are relevant for analyzing the feasibility of solving the problem. Each subset S is represented by the grouping of nodes in red.
Figure 2. Representation of the subsets N
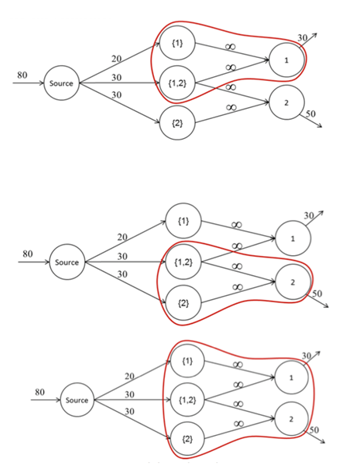
In the first subset, the total demand is 30 agents, and the sum of the capacities of incoming arrows is 50. In the second subset, the total demand is 50 agents, and the sum of the capacities of the incoming arrows is 60 agents. In the third and final subset S, the total demand is 80 agents, and the sum of the capacities of the incoming arrows is 80 agents. Therefore, as in all S subsets, the sum of the demands is less than, or equal to, the sum of the capacities of the incoming arrows. In general terms, this reasoning shows that, for a problem with two skills, with demands d1 and d2, the following restrictions must be met in order to obtain a solution for availability of agents c{1}, c{2} and c{1,2}:
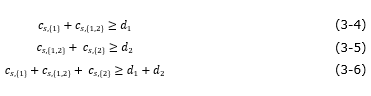
Generally, for any number of skills, we found that it is possible to allocate agents to skills if, and only if, for each subset L of the subset skill set H, the sum of available agents with compatible profiles, with at least one skill in L, is greater than or equal to the total demand of L. The formula (2-1), (3-2), (3-3) proposed in this paper is based on this principle to ensure that the allocation of agent profiles to call types can be met in each time interval.
4. Numerical Experimental (real data)
In this section, a realistic example is presented.
For the case study, we looked for a call center that delivers an inbound service, with a business model that would allow for the implementation of segmentation by skills, and that could provide data related to call volumes and operating costs. The study was conducted in a medium-sized Brazilian call center, which provides customer service and receives calls in Portuguese, English, and Spanish. Since these are the existing types of calls, call agents must be able to speak in the respective language.
4.1 Case study
The call center that was studied had the following agent profiles or skill sets and respective monthly costs:
• Monolingual: speaks only one language and can answer Portuguese calls only. Average monthly cost: R$ 800.
• Bilingual (Portuguese/English): speaks two languages fluently and can answer calls in Portuguese and English. Average monthly cost: R$ 1,200.
• Bilingual (Portuguese/Spanish): speaks two languages fluently and can answer calls in Portuguese and Spanish. Average monthly cost: R$ 1,200.
• Trilingual: speaks three languages fluently and can answer calls in Portuguese, Spanish and English. Average monthly cost: R$ 1,600.
In this call center, the information system forecasts and call volume forecasts are exported to an electronic spreadsheet. The prediction is based on intraday intervals of 30 minutes. Once the prediction is made, sizing is done on an electronic spreadsheet through applying the Erlang C formula. The call center’s service hours are from 8 am to 8 pm, with two 6-hour work shifts, one starting at 8 am and another at 2 pm. After sizing is completed, the management determines the time interval with the greatest demand for agents and uses this information to determine the number of agents needed per shift.
There were some notable drawbacks to this particular management method that drew our attention. The first is that there are too few work shifts and, consequently, more agents are needed to meet full demand during this call center’s peak intervals. If the company were to use hourly shifts instead, starting every hour from 8 am on, which is when the service begins, the agents’ shifts could be set up in such a way that it would be possible to meet the demand of calls during peak hours, while using fewer agents from the overall pool of employees. The call center does not currently do this, and scheduling of shifts is done manually, which complicates this procedure considerably.
The second drawback is that the planning method does not take certain situations into account, such as time intervals when there is a surplus of available agents with more than one skill. At those times, the extra manpower is wasted, since agents are not being scheduled to fill other available slots for agents with another skill. In other words, in reality, the benefits of being a skills-based call center are not being maximized, in that agents with bilingual (English-Portuguese) conversational skills are slotted merely to meet the demand for agents who can speak English. Furthermore, only monolingual agents are used to meet the demand in Portuguese. Finally, trilingual agents are generally not used because they require a higher salary. However, in some situations, it is possible that an optimal allocation would include trilingual agents. In the experiments presented below, it can be seen that the optimal allocation did not, in fact, include trilingual agents, but in the call center study, this possibility was not even considered, as shown in Table 1, which displays the forecasted demand provided by the call center. Following, is the plan made by the call center, which is patterned after the procedure described above regarding numbers of agents needed:
Table 1. Demand versus Call Center Plan
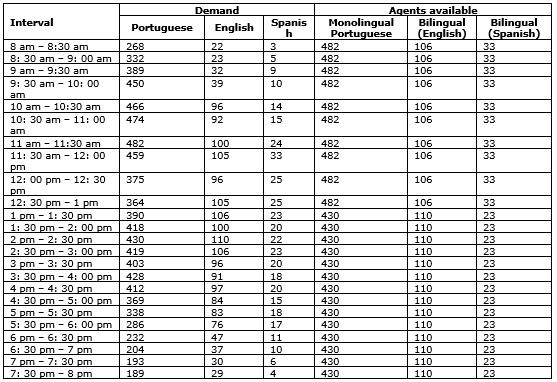
As can be seen, a lot of “idle time” exists with this type of planning, since there are an unnecessary number of agents on duty during periods of low demand. According to this plan, 912 (482 + 430) monolingual agents, 216 (106 + 110) bilingual Portuguese/English agents and 56 (33 + 23) bilingual Portuguese/Spanish agents need to be on staff. The total cost of the agents’ salaries, based on the average wage per agent profile, was R$ 1,056,000.
The program was implemented and solved by the ILOG CPLEX Optimizer (IBM, 2010) computational package, consistently using an execution thread. UFFLP (2012) was also used as an interface for implementing the programs. UFFLP is a library that provides an interface for Mixed, Integer and Linear Programming, and simplifies the integration with a resolver. The program was run on a computer with a 3.1 GHz processor, 4 GB of RAM and Microsoft Windows 7 64-bit operating system (MICROSOFT).
4.2 Results and Discussion
In the first round of testing, seven shifts were created, beginning every hour from 8 am until 2 pm, with breaks and intervals disregarded. Forecasting was done in intraday time intervals of 30 minutes. The same forecast and method were used for sizing to determine the number of agents per intraday time interval used in the analysis from the previous section, in order to have a basis of comparison. In both formulas, the results in numerical terms were equal, and the problem was solved in less than 0.01 seconds, generating the result displayed in Table 2.
Table 2. Number of Agents per Shift and Number of Skill Sets after Optimization
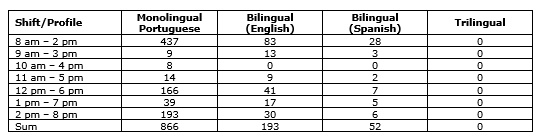
The above model suggests that the additional cost of working with trilingual agents is not worth the investment. The total cost of the solution obtained through the optimization package was R$ 985,600. When compared with the schedule planning used by the company, there is a saving of approximately 7% on labor-related costs (and maintaining the quality of service). The economy of scale can be attributed primarily to the greater number of possible shifts, since the agents can start work shifts every hour, as opposed to having only two different shifts. Moreover, as the following analysis shows, the model was also able to incorporate the flexibility of skill-based planning, thus reducing the number of agents needed. Table 3 compares intraday demand with the number of agents available in each time interval.
Table 3. Demand versus Agents Available per Time Interval after Optimization
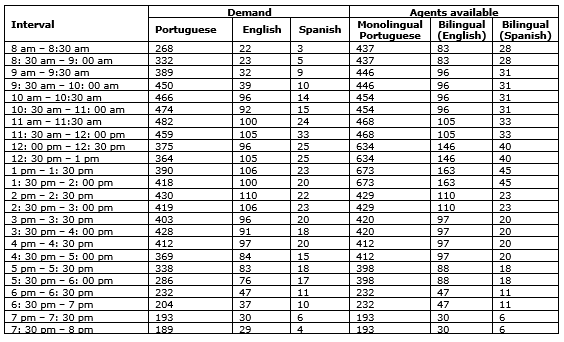
It is worth noting the interval between 3:30 pm and 4 pm: the demand for agents with Portuguese language skills is 428. However, there are only 420 monolingual agents available. However, the program makes use of the surplus of six bilingual Portuguese-English agents and two bilingual Portuguese-Spanish agents to meet the demand of calls in Portuguese. Thus, the model, aside from being robust, is capable of incorporating skills-based routing to provide optimal results, which is a significant step forward in comparison to the other shift scheduling models available to date.
Straightaway, we did another test of the model, this time seeking to incorporate labor law restrictions in order to obtain even more precise results. Labor legislation for this sector requires that during 6-hour shifts there must be two 10-minute breaks, the first one after the first hour of work and the second one before the last hour of work. Both breaks count as time on the job. There must also be an interval of twenty minutes between these two breaks, which does not count as time on the job.
For the second test, intraday demand was divided into 15-minute intervals. The 10-minute breaks were rounded off to 15 minutes, and the 20-minute breaks to 30 minutes. This "rounding off" is deemed reasonable because, in reality, there is a preparation time before work starts that is not counted as part of the break. Thus, the shifts are no longer considered uninterrupted work periods. There are, therefore, short intervals of time during working hours where agents are not fully on the job. It should be noted that a shift beginning at 8 am will end at 2:20 pm, not at 2 pm, as previously stated, since the 20-minute interval between breaks is not counted as part of the shift. We generated 275 different combinations of breaks and intervals, in accordance with the labor laws, and from these combinations, 1,925 different shifts were generated, starting every hour from 8 am to 2 pm.
The results were very similar to the ones from the previous experiment in terms of order of magnitude of the number of agents needed and consistency of the solution, as well as ensuring that every call will be answered by an agent with the required skill. For the sake of brevity, the table with the breakdown of the results was not included.
In this situation, the optimization package was able to find the optimal solution after 4.21 seconds for the first formula, based on the work of Bhulai et al. (2008), and in 0.89 seconds for the formula proposed in this paper. This suggests that the proposed model provides a better runtime, even for a considerably larger change in the parameters initially applied. Since the number of restrictions for the proposed formula grows exponentially according to the number of existing skills, the proposed model tends to have better performance, especially in situations where there are a large number of time intervals and relatively few skills.
The total cost of the solution was R$ 962,000 (even less than the first experiment), representing a saving of almost 9% in relation to the current cost. This is due to the fact that, despite the existence of pauses and breaks throughout the agent’s work shift, the overall duration is longer since the interval does not count as time on the job. The program managed to accommodate the breaks and intervals of the agents within the universe of existing combinations during the periods of low demand, so there was no need to allocate more agents to cover these breaks.
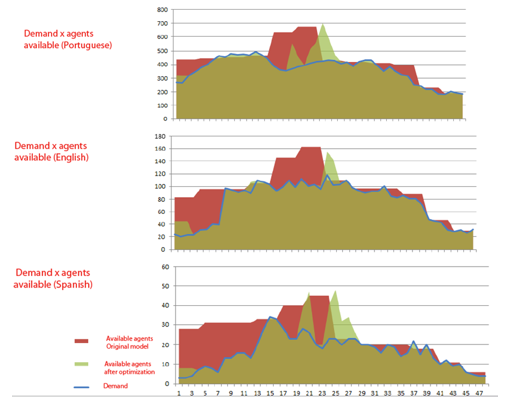
By analyzing the graphs in Figure 3, it can be seen that with the shifts generated by the optimization model for skill sets, it is possible to meet demand much more effectively and significantly reduce the amount of "idle time" agents will have on the job. In figure 3, the x is hour and; y-axis demands agents.
Figure 3. Demand versus Agents available for each language
5 Conclusion
As a result of this study, we were able to confirm that, in the situations tested, the proposed model was capable of efficiently solving the problem of scheduling agents in multi-skilled call centers within a relatively low computational time. Thus, the approach proposed in this study presents an alternative worthy of consideration, since it is able to successfully incorporate the flexibility of call centers with skills-based routing in an easy-to-implement model that has proven effective in experiments conducted in on-the-job settings.
There are some points that should be noted. As previously mentioned, this model suggests that a multi-skilled agent is capable of providing as good a service – within the same call time frame – as an agent who specializes in a particular type of call. In the case of the call center we studied, this assumption proved true, because the only "specialized" agents in the call center are monolinguals who are only able to answer calls in Portuguese. The multi-skilled bilingual and trilingual agents are Brazilian, so they have the same ability to answer Portuguese calls as the monolinguals.
Another point that should be taken into consideration is the number of times the test was run. It would be necessary to run tests on a larger scale, with more combinations of shifts, to be able to confirm the model’s efficiency. In conclusion, the approach presented in this research has characteristics that can be considered unprecedented and, for this reason, warrants a more thorough analysis. Therefore, more detailed research is necessary, which is why the "case study" methodology was adopted.
As previously stated, the work of Wallace et Whitt (2005) suggests that it is not efficient to create groups of multi-skill agents with more than two skills. Therefore, even if testing on a larger scale was needed, the number of skill combinations would continue to be relatively low. Lastly, the model introduced in this study, as well as the work of Bhulai et al. (2008), uses an approach based on the Set Cover problem, and there is ample literature that confirms that these problems are successfully solved by the optimization packages available on the market.
Nonetheless, the results of this research provide a new proposal for the use of operational research to solve management-related problems in call centers. It is believed that this model may be able to solve other problems related to allocation of supply and demand.
References
Aguir, M. S.; Aksin, O. Z.; Karaesmen, F.; Dallery, Y. (2008), “On the Interaction between Retrials and Sizing of Call Centers”. European Journal of Operational Research; Vol. 191, No. 2, pp 398-408.
Aksin, O. Z. et Harker, P. T. (2003) “Capacity Sizing in the Presence of a Common Shared Resource: Staffing an Inbound Call Center”. European Journal of Operational Research; Vol. 147, No. 3, pp 464-483.
Aksin, O. Z.; Karaesmen, F.; Ormwci, E. L. (2007), A Review of Workforce Cross-Training in Call Centers from an Operations Management Perspective. In: Nembhard, D. A (Ed), Workforce Cross Training Handbook. USA: CRC Press.
Aktekin, T. (2014), “Call Center service process analysis: Bayesian parametric and semi-parametric mixture modeling”. European Journal of Operational Research; Vol. 234, No. 3, pp 709-719.
Atlason, J.; Epelman, M.; Henderson, S. (2004), “Call center staffing with simulation and cutting plane methods”. Annals of Operations Research; Vol. 127, Pp. 333-358.
Avramidis, A. N; Chan, W.; Gendreau, M. et al. (2010), “Optimizing Daily Agent Scheduling in a Multiskill Call Center”. European Journal of Operational Research; Vol. 200, No. 3, pp. 822-832.
Barbosa, D. S. F. B. (2011), ”Responsabilidade Civil no serviço de atendimento ao consumidor e a culpa contra a legalidade”. Available from: http://jus.com.br/artigos/18951/responsabilidade-civil-no-servico-de-atendimento-ao-consumidor-e-a-culpa-contra-a-legalidade Accessed on July 26, 2014.
Bertsimas, D. et Xuan, V. D. (2010), “Robust Data-driven Approaches to Call Centers”. European Journal of Operational Research; Vol. 207, No. 2, pp. 1072–1085.
Bhulai, S.; Koole, G.; Pot, A. (2008), “Simple Methods for Shift Scheduling in Multi-Skill Call Centers”. Manufacturing & Services Operations Management; Vol. 10, No. 3, pp. 411-420.
Brown, L.; Gans, N.; Mandelbaum, A. et al. (2005), “Statistical Analysis of a Telephone Call Center: A Queueing-Science Perspective”. Journal of the American Statistical Association; Vol. 100, No. 469, pp 36-50.
Callcenterinf (2012). Available at: http://www.callcenter.inf.br. Accessed on July 15, 2015.
Cezik, M. et L’Ecuyer, M. P. (2008), “Staffing. Multiskill call centers via linear programming and simulation”. Management Science; Vol. 54, No. 2, pp. 310-323.
Channouf, N et L’Ecouyer, P. (2012), “A normal copula model for the arrival process in a call center”. International Transactions in Operational Research; Vol. 19, No. 6, pp. 771-787.
Cordone, R.; Piselli, A.; Ravizza, P.; Righini, G. (2011), “Optimization of Multi-Skill Call Centers Contracts and Work-shifts”. Service Science; Vol. 3, No. 1, pp. 67-81.
Dantzig, G. B. (1954), “A comment on Edie’s “traffic delays at toll booths”. Operations Research; Vol. 2; No. 3, pp. 339-341.
Dietz, D. C. (2011), “Practical Scheduling for Call Center Operations”. Omega; Vol. 39, No. 5, pp. 550-557.
Dietz, D. C. et Vaver, J. G. (2006), “Synergistic modeling of call center operations”, Journal of Applied Mathematics and Decision Sciences, Vol. 2006.
Dudin, S.; Kim, C., Dudina, O. et al. (2013), “Queuing System with Heterogeneous Customers as a Model of a Call Center with a Call-Back for Lost Customers”. Mathematical Problems in Engineering, Vol. 2013.
Fiems, D.; Maertens, T.; Bruneel, H. (2008), “Queueing systems with different types of server interruptions”. European Journal of Operational Research; Vol. 188, No. 3, pp 838–845.
Gale, D. (1957). A Theorem on Flows in Networks. Pacific Journal of Mathematics; Vol. 7, No. 2, pp. 1073-1082.
Gans, N.; Koole, G.; Mandelbaum, A. (2003), “Telephone call centers: Tutorial, review, and research prospects”. Manufacturing Service Operations Management, Vol. 5, No. 2, pp. 73–141.
Gong, J.; Yu, M.; Tang, J. (2015), “Listaffing to Maximize Profit for Call Centers with Impatient and Repeat-Calling Customers”, Mathematical Problems in Engineering; Vol. 2015.
Jouini, O.; Dallery, Y.; Aksin, Z. (2009), “Queueing Models for MultiClass Call Centers with Real-Time Anticipated Delays”. International Journal of Production Economics; Vol. 120, No. 2, pp. 389-399.
Kim, J. W. et Park, S. C. (2010), “Outsourcing strategy in two-stage call centers”. Computers & Operations Research; Vol. 37, pp. 790-805.
Koole, G. (2010), Optimization of Business Processes: an introduction to applied stochastic modeling. Vrije Universiteit Amsterdam. Available at: http://www.math.vu.nl/~koole/obp/obp.pdf . 2010 Accessed on Feb 23, 2012.
Koole, G. (2013), Call Center Optimization. MG Books, Amsterdam.
Legros, B.; Jouini, O.; Dallery, Y. (2015), “A flexible architecture for call centers with skill-based routing”. International Journal of Production Economics, Vol. 159, pp. 192-207.
Pinedo, M. L. (2005), Planning and Scheduling in Manufacturing and Services. Springer, New York, NY, USA.
Reynolds, P. (2003), Call Center Staffing: The Complete, Practical Guide to Workforce Management. The Call Center School, Lebanon, TN, USA.
Robbins, T. R. et Harrison, T. P. (2010), “A stochastic programming model for scheduling call centers with global service level agreements”. European Journal of Operational Research; Vol. 207, No. 3, pp 1608-1619.
Rolfini, F. (2013), Brasil já é 7º maior PIB do mundo em serviços de contact center, Available at: https://goo.gl/HKoqh7 Accessed on Oct 10, 2014.
Sawik, T. (2010), “Single vs. multiple objective supplier selection in a make-to-order environment”. Omega; Vol. 38, No. 3-4, pp. 203-212.
Stolletz, R. (2003), Performance Analysis and Optimization of Inbound Call Centers. Springer-Verlag. Berlin, Germany.
Thompson, G. (1997), “Labor staffing and scheduling models for controlling service levels”. Naval Research Logistics; Vol. 44, No. 8, pp. 719-740.
Tjosvold, D.; Chen, N. Y.; Huang, X. (2014), “Developing Cooperative Teams to Support Individual Performance and Well-Being in a Call Center in China”; Group Decision Negotiation, Vol. 23, pp. 325-348.
Wallace, R. et Whitt, W. (2005), A Staffing Algorithm for Call Centers with Skill-Based Routing. Manufacturing & Service Operations Management; Vol. 7, No. 4, pp. 276-294.