Evaluation of Total Oil and Grease with Flow Control for Mature Oil Fields in the Context of Industry 4.0
Juracy Leandro do Nascimento
juracyln@hotmail.com
Petróleo Brasileiro S.A. - Petrobras, Macaé, Rio de Janeiro, Brazil.
Alessandro Copetti
alessandro.copetti@gmail.com
Fluminense Federal University – UFF, Rio das Ostras, Rio de Janeiro, Brazil.
Luciano Bertini
lbertini@id.uff.br
Fluminense Federal University – UFF, Rio das Ostras, Rio de Janeiro, Brazil.
Patrick Barbosa Moratori
pmoratori@gmail.com
Fluminense Federal University – UFF, Rio das Ostras, Rio de Janeiro, Brazil.
Mário Cesar Mello Massa de Campos
mariocampos@petrobras.com.br
Petrobras Research Center - CENPES, Rio de Janeiro, Rio de Janeiro, Brazil.
ABSTRACT
Goal: Industry 4.0 enables the design of new models for process monitoring in which sensors, analyzers, and controls are positioned at different points in the process. The goal of this work is to present the modeling and control of a three-phase production separator with hydrocyclones to treat produced water on an oil platform of mature fields.
Design / Methodology / Approach: The Methodology or approach used was to develop a model for the primary separator that allows its operation by means of a controller (fuzzy and PI) to manipulate the flow of discarded water, acting indirectly in the oil-in-water measure.
Results: The results showed the consistency of the model for open loop simulations and the effectiveness of the controllers to comply with the discarding requirements for the closed-loop simulations.
Limitations of the investigation: The limitation of the model and developed controllers is that they are only applied to platforms where water production exceeds the separators discharge capacity and the exceeding water can be offloaded to another equipment or to another platform.
Practical implications: The main practical implications of this study are to maximize the flow of discarded water on mature field platforms, which produces elevated amounts of water, to conform the total oil and grease to the local law regulations. Additionally, it also increases oil production, with a higher limit of water production.
Originality / Value: Compared to the previous authors, where the models of discarded flow is a function of the water-oil interface, this work developed a model that allowed the flow of the discarded water to be a function of its quality.
Keywords: Industry 4.0; Primary oil processing; Produced water; Fuzzy control; PID control.
INTRODUCTION
Research in the area of oil and gas is noticeably scarce, since it is an area of specific processes whose managers are more closely linked to this industry than to the academy. In the area of Integrated Operations (IO), the work presented in Lima et al. (2015) stresses the importance of integrating people, processes, and technologies, to make faster decision-making based on real-time data. In Castro et al. (2015), the importance of the integration between portfolio, projects, production operations, and resource allocation is also addressed, adding value to an organization. Both papers are literature reviews that emphasize the importance of production optimization with real-time data and process automation, which is the objective of this article. This research automates a task that until now was performed manually and with significant delays in decision-making, in the order of hours. In Martins et al. (2018), another review of the literature is presented, integrating reliability concepts with Condition Based Maintenance and Prognostic Health Management, applied in the prevention of blow-out in oil production wells. Improving control systems, which is the purpose of this paper, is as important as improving reliability, and is also a goal of the future integrated industry. This work applies the aforementioned concepts to optimize the treatment of oil on production platforms.
Oil is extracted from natural reservoirs in a multiphase form, containing oil, gas, and water. The platform that obtains this mixture will perform the method known as primary oil processing.
Primary oil processing is the first separation step to which oil is subjected as soon as it reaches the surface. At this stage, the three phases are separated in the gravitational separators. In addition, it is still necessary to treat the oily phase to reduce the emulsified water content and the salts dissolved therein so as to satisfy the minimum export requirements. The gaseous phase also needs to be treated to reduce the water (vapor) content and other contaminants so that it is sent to treatment terminals by means of a pipeline. In addition to oil and gas, produced water also requires treatment for disposal at sea or reinjection (Brasil et al., 2014).
In the context of primary oil separation, produced water is the water from the well that reaches the sea surface and must be treated. Discarded water is the one that will be disposed into the sea after proper treatment. This work specifically investigates the water–oil separation system, with a focus on maximizing discarded water, since this is a necessary operation in mature oil fields.
The amount of produced water is aggravated during oil extraction. In order for oil production in the producing wells to not be reduced rapidly, it is crucial that water be injected into the reservoir to maintain its pressure. This water, which is injected through injector wells, is eventually produced as a byproduct along with petroleum. Therefore, in mature fields, the production of water increases, which hinders the process and reduces the economic useful life of the field. In addition, as the oil industry has evolved and increased its production, requirements for water (TOG: total oil and grease content) and oil export (BSW: basic sediment and water) have become more restrictive (the TOG for water discard must be less than 29 ppm, according to Art. 5 of Resolution 393/07 of Brazilian National Environment Content (Conselho Nacional de Meio Ambiente – CONAMA) and the BSW for export must be less than 1% according to the Joint Resolution ANP / Inmetro no.1 of June 10, 2013), and the improvement of equipment and control strategies is required. Technologies for oil and water treatment, such as hydrocyclones, floats, and dual-polarity and dual-frequency tracers, have emerged. These technologies have introduced greater complexity into plants. Consequently, the area of process control has also evolved.
In this context, some authors have developed phenomenological models based on mass and momentum balances that, together with population balances, made it possible for one to estimate the dispersion separation efficiencies, simulate the separation systems, and test the control strategies (Nunes, 2007). These models supported the development and optimization of control strategies. It is important to emphasize that the works of Nunes (2007), Filgueiras (2005), Silveira (2006), Ribeiro et al. (2016), and Backi et al. (2018), dealing with the modeling of production separators, consider the realization of interface control in the separation chamber, where all available water is separated. The control that is performed is thus efficient; however, in many cases, it is not implemented for practical reasons, as will be explained below.
The problem addressed in this work is the difficulty of treating the produced water in mature fields owing to the increase in the BSW of the produced oil, and consequently the increase in the water flow. On several platforms, it is not possible to discard all free water from the production separator within the requirements defined by law owing to the limitation of the treatment system. Thus, the discarded flow is manually limited, and the rest of the water follows with the oil phase to be withdrawn in another piece of equipment or even on another platform. In such cases, a certain opening in the water outlet control valve of the separator is manually adjusted. This opening should generate a discharge water flow so that the treatment system can satisfy the defined requirements. In practice, this flow is not always optimized, and the excess water that remains along with oil eventually overloads the treatment on electrostatic handlers or on other platforms.
The objective of this work is to propose a controller for the water discharge rate that considers its quality, measured in terms of the TOG, and applies it to cases in which it is not possible to perform the water–oil interface control owing to the excess of produced water. The proposed controller aims to maximize the flow of discarded water while maintaining the requirements established by legislation. Accordingly, the strategy adopted consists of modeling the three-phase horizontal production separator, considering that only part of the free water that arrives in the production separator will be discarded.
In order to meet the proposed control strategy, two innovations will be applied, considering Industry 4.0. Firstly, the use of TOG meters is required. Early models of TOG meters displayed a number of operational problems. The advancement of technology, however, has enabled the creation of more robust sensors that allow the use of this control strategy. Second, to test the proposed controller, modifying the conventional models mentioned was mandatory.
This paper presents a simplified model of a primary processing unit and produced water treatment composed of a production separator and a battery of hydrocyclones. The production separator is modeled by modifying the model proposed by Nunes (2007) and Backi et al. (2018). Their approach considered separators in which water-oil interface control and discharge flow were determined by the water–oil separation kinetics in the separator. Since this work proposes the use of a TOG controller instead of the interface control, it needs a model that would allow the flow of the discarded water be a function of its quality.
Additionally, two controllers will be tested for the quality of the discarded water, whose manipulated variable will be the discard rate. The controllers chosen were a conventional proportional integral control (PI) and a fuzzy proportional derivative control (fuzzy PD). Finally, both controllers will be compared considering the discharge flow and the setting of the quality parameters of fluids produced within the requirements permitted by law. The PI controller is the most common in the industry and is applied to slow processes. Furthermore, as the fuzzy controller can be designed to behave according to the human deductive reasoning, it can take actions based on specialist knowledge.
The proposed solution develops a new approach for the control of oil-in-water concentrations in the processes of primary oil separation, based on an integrated view, made possible by industry 4.0. The application of these controllers will lead to the maximization of discarded water flow in the production separators of mature field platforms. That will occur without overloading equipment downstream and while maintaining the requirements imposed by legislation; it can possibly provide oil production gains.
PRIMARY OIL PROCESSING
Oil is a naturally occurring blend. It consists predominantly of hydrocarbons and organic sulfur, nitrogenous, and oxygenated products. It is apparently a homogeneous substance; however, it contains a mixture of liquid and solid gases whose characteristics vary according to the producing field. Thus, petroleum, in its natural state and at room temperature, is a dispersion of gases and solids in a liquid phase and may be in the Newtonian or non-Newtonian state as a function of temperature (Farah, 2012).
Fluid streams from different wells that arrive through production manifolds to the surface, on land or on platforms, are not yet suitable for use or export. In addition to the oil and gas phases, an oil well usually produces water after a certain time of operation, either because it is initially present in the reservoir, or by its injection, in a process aimed at maintaining the reservoir pressure, i.e., the increase in oil recovery. Thus, it is essential that maritime or terrestrial fields be equipped with production facilities for the gas–oil–water separation (Kunert, 2007).
In marine fields, primary oil processing is usually performed on oil production platforms. Initially, primary separation of the fluid streams produced is performed and, subsequently, the gas, oil, and water phases are individually treated. The oil phase is used to reduce the emulsified water content and the salts dissolved therein; the gaseous phase is treated to reduce the content of water and other contaminants; the water phase is separated from the oil for disposal or reinjection into producing wells. This treatment during the production aims to satisfy the oil and gas export requirements as well as the requirements for the disposal of produced water (Brasil et al., 2014).
In order to satisfy legal requirements, oil production platforms rely on a processing plant that normally contains gravitational separating vessels in series or in parallel and can have various configurations depending on the desired separation quality or the characteristics of the fluids produced.
The water from the gravitational separators is sent to the water treatment plant. This unit may contain hydrocyclones and floats. Hydrocyclone is a static piece of equipment in a conical format with the function of reducing the oil content of water. Floats are vessels where microbubbles that aggregate the oily particles present in the water and carry them to the surface are produced.
Gravitational fluid separation
This is the first stage of the primary oil processing, at which each of the fluids present in the oil is separated owing to the difference of density between the phases in a cylindrical pressure vessel (gravitational separator). The separators can segregate two or three phases, depending on whether it is desired to separate the free water, and can be horizontal or vertical. In addition to phase separation, these vessels have the function of absorbing the oscillations in the production flow of the wells (Filgueiras, 2005). In this work, a horizontal three-phase production separator will be modeled (See Figure 1).
Figure 1. Three-phase horizontal separator
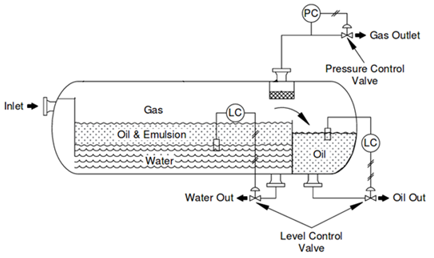
Source: adapted from Arnold and Stewart (2008).
In the three-phase separators, there is a spillway that delimits the separation zone of the oil chamber. In the separation chamber, there remain gas droplets, which, upon release, migrate to the gas phase. Further, as the aqueous phase is denser than the oil phase, it tends to move to the bottom of the separation chamber, from where it is withdrawn. The oil migrates to the top of the separation chamber and flows into the oil chamber, where it is also removed. The separation chamber can rely on wave breaking baffles, which are devices used to reduce the effect caused by the platform’s balance, or coalescing plates, which are parallel plates that promote the coalescence of the dispersed phases (Arnold and Stewart, 2008).
Notably, there must be sufficient residence time in the vessel for the separation of the water and oil phases to occur. Thus, the equipment must be designed properly. The lower the flow, the longer the residence time is, and consequently, the greater the separation is.
The design and dimensioning of this equipment is based on Stokes' law, which calculates the terminal velocity of the dispersed phase droplets. This law is shown in Equation 1.
where
ρc: density of the aqueous phase;
ρd: density of the oil phase;
d: diameter of the dispersed phase droplets;
µc: viscosity of the continuous phase;
ν: terminal drop velocity of the dispersed phase in the continuous phase.
From Equation 1, it becomes observable that the greater the difference in density between oil and water, the larger the dispersed phase droplets. Alternatively, the lower the viscosity of the continuous medium, the easier the separation in the three-phase gravitational separator will be.
PROPOSED MODEL
Nunes (1994) developed a mathematical model of the three-phase separator. Their model achieves the separation processes of water–oil and oil–water emulsions, considering the thermodynamic phase equilibria and the interference of the vessel control. Nunes analyzed the performance of the separator through studies of the parameters of the controllers, the variations of the loads, and the geometry of the internal devices of the vessel. The work of Nunes (2007) presents a simplification of the model of Nunes (1994) by eliminating the need for the calculation of thermodynamic equilibrium.
Filgueiras (2005) continued the work of Nunes (1994) and Nunes (2001). The three-phase separator model proposed by the author uses the Nunes (1994) model with some simplifications: the phase densities are the same, the thermal effects are neglected, the internal devices considered are parallel plates, and there is no liquid drag through the gas phase.
Yayla et al. (2017) developed a two-dimensional computational fluid dynamics model for coalescing plates to investigate the influence of the flow type and the shape of the plates on the separation efficiency.
Othman et al. (2018) make a theoretical and experimental investigation of a horizontal pipe separator, presenting a model that considers mixture velocity and BSW in the separation efficiency calculation.
Backi et al. (2018) also use a simple production separator model for controller design and estimation of non-measurable parameters and disturbances. As in the Nunes (2007) model, Backi et al. (2018) incorporate three dynamic state equations describing the levels of the global liquid (water plus oil) and water as well as the gas pressure subject to input and output dynamics. In addition, algebraic equations that calculate simplified droplet distributions for each continuous phase are introduced to determine the exchange of water and oil between the two continuous phases.
This work is based on the models proposed by Nunes (2007), Filgueiras (2005), and Backi et al. (2018). Adaptations were made in order to allow representation of the production separators whose discharge flow is limited by the quality of the discarded water and not by the water–oil separation kinetics. Thus, if control of this interface is achieved, the flow of discarded water would be higher than the flow at which the treatment system can satisfy legal requirements. Therefore, this model can only be applied to separators whose water–oil emulsion presents easy separation and if the separated oil in the oil chamber has free water.
Figure 2 shows the system that will be modeled. This system will require an in-line TOG meter installed in the water outlet of the hydrocyclones. The control of TOG will be performed by controlling the flow of water discarded by the separator. The proposed controller will receive the TOG meter signal and act on the valve located downstream of the hydrocyclones—i.e., the controlled variable is the TOG in the hydrocyclones water outlet flow and the manipulated variable is the opening of the water discard valve. If the TOG shows a value above the setpoint, the water discard valve closes, increasing the residence time of the water in the separator and reducing the TOG value to the setpoint. If the TOG is below the setpoint, the discharge valve opens, the flow rate is discarded, and the TOG increases.
Figure 2. Control of the TOG at the hydrocyclone outlet with the water discard valve

Source: adapted from Filgueiras (2005).
A change adopted in this model was the estimation of the volume where the coarse water–oil separation occurs, i.e., the volume where the complete separation of the mixture has not yet occurred and which was not considered in the calculation of the residence time of the production separator’s water chamber (see Equation 2).
where
Vecs: emulsion volume in the separation chamber;
Lin: oil phase inlet flow rate;
Win: water phase inlet flow rate;
Tsep: separation time of the oil–water mixture.
Equation 3 shows the volume of the separation chamber whereas equations 4 and 5 show the volumes of the oil chamber and the gas phase, respectively. These equations were developed from geometric relations.
where
Vcs: volume of the separation chamber;
Vcl: volume of the oil chamber;
Vt: total volume of the separator;
D: diameter of the separator;
Ccs: length of the separation chamber;
Ccl: length of the oil chamber;
hw: height of the weir;
hl: height of liquid in the oil chamber.
The volume of the aqueous phase in the separation chamber is calculated by obtaining the difference between the separation chamber volume and the water–oil mixture volume, as shown in Equation 6.

where
Vwcs: volume of water in the separation chamber.
Equations 7 and 8 were developed through the mass balance in the oil chamber and the space occupied by the gas. The variation of the height in the oil chamber is given by Equation 7.

where
Win: inlet flow rate of the water phase;
Lin: inlet flow rate of the oil phase;
Wout: outlet flow rate of the separation chamber;
Lout: outlet flow rate of the oil chamber.
The pressure variation in the vessel is given by Equation 8.

where
Gin: inlet gas flow rate;
Gout: outlet gas flow rate;
p: pressure.
Equation 9 shows the variation of the volume of water in the oil phase of the oil chamber.
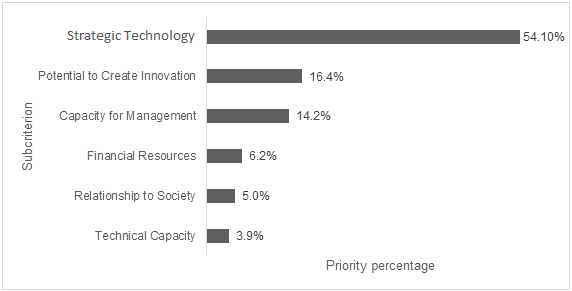
where
Vwcl: water volume in the oil chamber.
The outlet flows of water, oil, and gas are defined by the opening and characteristics of the control valves. The correlations obtained in the Masoneilan valve manufacturer’s control valve designing handbook (2000) were used to calculate the valve flow rates. Equations 10, 11, and 12 express the outlet flows of water, oil, and gas, respectively.
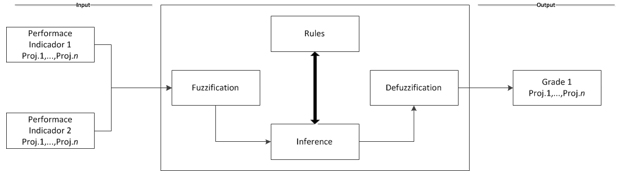
where
Cvmaxw: maximum discharge coefficient of the gas valve;
Cvmaxl: maximum discharge coefficient of the oil valve;
Cvmaxg: maximum discharge coefficient of the water valve;
sw: viscosity of the continuous phase;
sl: opening fraction of the oil valve;
sg: opening fraction of the water valve;
dw: specific gravity of water;
dl: specific gravity of oil;
dg: specific gravity of gas;
MWg: molecular weight of gas;
pjus: pressure downstream of oil and water valves;
pcomp: pressure downstream of gas valve;
R: gas constant;
T: temperature;
ρw: specific mass of oil;
ρl: specific mass of water.
To estimate the TOG of the stream of water leaving the production separator, an alternative model to the separation efficiency model based on the phenomenological modeling presented by Nunes (2007) will be adopted. Nunes et al. (2010) used platform operation data to generate an experimental correlation for TOG calculation. Accordingly, they evaluated the TOG of the discarded water at three different water interface oil heights in the separation chamber and constructed a TOG curve × water residence time. This model was used in this study. Nunes et al. (2010) proposed Equation 13.
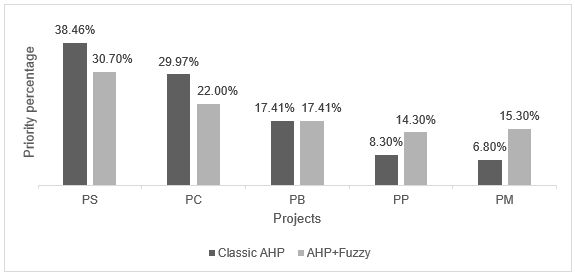
where
TOGSG: TOG in the water outlet of the production separator;
TR: residence time of the aqueous phase, which is calculated using Equation 14.

For the calculation of the separation efficiency in the hydrocyclones, a correlation developed by Nunes and Lima (2006) was used for a given hydrocyclone geometry and drop diameter distribution. This correlation is shown in Equation 15.

where
A: 3619.6 – 1775039.5 • Wout;
b: 208.9;
Split: ratio between overflow and underflow in hydrocyclones.
After calculating the efficiency, the TOG at the hydrocyclone’s exit is calculated by using Equation 16.

where
TOGH: TOG in the hydrocyclones’ water outlet.
RESULTS
This section analyzes the results of the models for the separator and the hydrocyclones. Additionally, the dynamic simulation verified the response of the proposed controllers to the variations in the the system’s inlet flows. The simulations were performed using MATLAB-Simulink version 2014a.
Production separator simulation
The data of flows and dimensions used in the simulation are of typical real equipment. Tables 1 and 2 show the dimensions of the separator and its physico-chemical parameters, respectively.
Table 1. Dimensions of the separator

Table 2. Physico-chemical parameters

The oil inlet flow rate is considered to be equal to the water inlet flow rate, i.e., the input BSW is 50%. The TOG × residence time curve, generated from Equation 13, is shown in Figure 3.
Figure 3. TOG at production separator output × residence time

Source: The authors themselves
As previously mentioned, the residence time is a function of the aqueous phase volume in the separator and the water discharge rate. The aqueous phase volume is given by the volume of the (constant) separation chamber subtracted from the volume of the emulsified layer of the separation chamber which, in turn, is a function of the inlet flow rate, according to Equations 2, 6, and 14.
The TOG curve at the production separator output × discarded water flow rate for different raw input flow rate (Qi) values is shown in Figure 4.
Figure 4. TOG at the production separator output × water discharge rate

Source: The authors themselves.
As expected, the TOG of the separator water outlet increases with the increase at the discarded water flow rate and at the inlet flow rate in the separator.
Hydrocyclones simulation
For the simulation of the hydrocyclones, it was necessary to define the number of liners (sections of conical tubes that compose the hydrocyclones) and the reject ratio. The number of liners was defined in order to maintain the flow rate within the acceptable range for hydrocyclones (2–6 m³/h). The reject ratio was defined so that TOG presented sensitivity to this change, with a discharge rate limited to the separator model. The number of established liners was 65, and the reject ratio was 4.9%. If the reject ratio is assigned a value greater than 5%, the discharge rate would be larger and beyond the range of the separator model. If it were assigned a lower value, the discharge rate would be lower, and the TOG variation would be less significant. Thus, an efficiency curve of the hydrocyclones with respect to the flow in each liner is drawn (see Figure 5).
Figure 5. Efficiency of hydrocyclones × flow rate per liner

Source: The authors themselves.
With the efficiency data of the hydrocyclones in relation to the flow rate per liner and TOG of the production separator output in relation to the discharge flow rate, it was possible to construct a curve of TOG at the exit of the hydrocyclones × discharge of water, which is shown in Figure 6.
Figure 6. TOG at hydrocyclone output × discarded water flow

Source: The authors themselves.
Dynamic simulation
This section shows the dynamic simulation developed to verify the actuation of the controllers against the variations in the inlet flows.
The proposed system model was implemented using an s-function in MATLAB, as was done in the works of Ribeiro (2012) and Silveira (2006). This choice is justified by the lower difficulty of solving the differential equations (integration with time) offered by this method. The maximum interval for the integration was 10 s, as in the work of Filgueiras (2005), and the minimum interval was in accordance to the automatic mode.
Two controllers were tested to guarantee the quality of the discarded water and to operate with the maximum flow of water. The controllers chosen were a PI and a fuzzy PD.
In addition to the proposed TOG control of discarded water, there are two other controllers: a level controller in the oil chamber and a separator pressure controller. PI controllers were adapted for both cases. Notably, the use of the PID controller is avoided for level and pressure, as the noise generated at the pressure and level measurement when associated with the derivative term of the controller can generate undesired actions.
The pressure setpoint adopted was 9 kgf/cm², the level setpoint was 1 m, and the TOG setpoint was 29 ppm. The initial conditions, controller parameters, and valve data used in the simulation are shown in Table 3.
Table 3. Parameters used for dynamic simulation

Source: The authors themselves.
Two experiments were performed to test the controllers. The first involved applying a step perturbation by doubling the inlet flow of the system, and the second consisted of applying a sinusoidal disturbance. In both cases, the input BSW was maintained at 50%. In the scenario of the application of the step perturbation, the gross inlet flow was initially 0.16 m³/s and reached 0.32 m³/s in 100 s. The simulation was performed up to 250 s. In the sinusoidal disturbance scenario, the amplitude was equal to 0.08 m³/s, the period was 180 s, and the average value was 0.24 m³/s. The disturbance started after 100 s of simulation and the total simulation time was 640 s. A dead time of 1 s was established between the controller output signal and the valve to simulate the valve delays, and a dead time of 10 s was established to simulate the TOG analyzer delay.
To evaluate the controllers, the average TOG in the simulation period, the highest TOG value, the time required for returning to the setpoint, and the integral of the absolute error (IAE) will be considered. The IAE is a performance index that calculates the magnitude of the absolute error integral (see Equation 17) and allows an objective comparison between the controllers.

Subsequently, the parameters of the proposed controllers (PI and Fuzzy PD) and the system response to the applied disturbances will be presented.
To simulate the PI controller, a proportional gain of 0.001, an integral gain of 0.0005, and an initial valve opening of 0.308 were used. The results of the step perturbation are presented in Figures 7 and 8, and the results of the sinusoidal perturbation are presented in Figures 9 and 10.
Figure 7 shows the PI control response for the step-type disturbance in the inlet flow. After 100 s of simulation, the peak of TOG at the exit of the separator occurs, owing to the increase in the volume without the complete separation between the phases. This effect is caused by the increase at the inlet flow rate. This indicates the reduction of the free water volume in the separation chamber and the reduction of the residence time, causing an increase in the TOG. As the discharge rate within 100 s had no variation, the efficiency of the hydrocyclones remained the same, and the TOG at the exit of the separator increased. Thus, the TOG at the hydrocyclones’s exit (right axis) also increased. The controller actuated the closing of the water discharge valve, and the TOG at the outlet of the separator stabilized at a lower value. The TOG at the exit of the hydrocyclones returned to the setpoint. The time required by the TOG of the discarded water to return to the normal value was approximately 41 s, its peak was 37.6 ppm, the TOG average was 29.7, and the IAE was 205.
Figure 7. Response of the TOG PI control to the step-type perturbation at the inlet flow rate

Source: The authors themselves.
In Figure 8, one is able to observe the closing of the water discharge valve owing to the action of the proposed quality controller, in response to the increase in TOG (on the right axis), and the reduction at the discharge flow rate (left axis). The mean flow rate discarded in the simulation time was 0.0616 m³/s.
Figure 8. Response of the discarded flow rate to the step-type disturbance at the inlet flow rate

Source: The authors themselves.
A sinusoidal disturbance was also applied to the inlet flow rate. As shown in Figure 9, after the onset of the disturbance, the TOG at the output of the separator increased owing to the increase at the inlet flow rate. However, as the increase was gradual, the controller acted to shut off the water outlet valve, reducing the flow of discarded water (as shown in Figure 10) and, consequently, the TOG peak was reduced. Subsequently, with the reduction in the inlet flow and consequent reduction in the TOG of the discarded water, the controller acted to open the valve and increase the discharge flow rate. This cycle was repeated with the same period of disturbance in the inlet flow. The peak was observed to be 32.3 ppm, the mean of the discarded TOG was 29 ppm, and the IAE was 989.
Figure 9. Response of the TOG PI control to the sinusoidal perturbation at the inlet flow rate

Source: The authors themselves.
Figure 10. Response of the discarded water flow rate to the sinusoidal disturbance at the inlet flow rate

Source: The authors themselves.
The fuzzy controller was defined as Mamdani type and defuzzified by the centroid method as well as Paiva et al. (2016). For implementation in MATLAB, a fuzzy module was used.
The fuzzy controller used was a fuzzy PD controller with two input variables, i.e., TOG and TOG variation (derived from TOG), and an output variable, i.e., the change in valve position. The control surface (shown in Figure 11) presents the action of the control valve (controller output signal) for each combination of input signals.
Figure 11. Control surface

Source: The authors themselves.
To simulate the system behavior with the fuzzy controller, the same perturbations and initial conditions of the PI controller case were applied. Figure 12 shows the response of the fuzzy PD controller to the step-type perturbation at the inlet flow rate.
Figure 12. Response of the TOG fuzzy PD control to the step-type perturbation at the inlet flow rate

Source: The authors themselves.
After 100 s of simulation (moment of the step application), the peak of TOG occurred at the exit of the separator and the exit of the hydrocyclones owing to the sudden increase in the flow. Similar to the PI controller, the fuzzy PD controller actuated the closing of the water discharge valve. Subsequently, the TOG at the output of the separator stabilized at a lower value, whereas the TOG at the output of the hydrocyclone returned to the setpoint (29 ppm). The time required by the TOG of the discarded water to return to the setpoint was approximately 46 s, the peak was 37.6 ppm, the average TOG was 30 ppm, and the IAE was 260. It was verified that, compared to that of the PI control, there was an increase in the time involved in reaching the setpoint, a reduction of the TOG mean, and an increase in the IAE. However, there was no change in the TOG peak, as the variation was instantaneous, and there was no time for the control to reduce TOG.
In Figure 13, the closing of the water discharge valve and restriction of the discharge flow can be observed. The mean flow rate discarded during the simulation was 0.0575 m³/s.
Figure 13. Response of the discarded flow rate to the step-type disturbance at the inlet flow rate

Source: The authors themselves.
A sinusoidal disturbance was applied to the inlet flow. The TOG controller response and the TOG at the production separator outlet flow are shown in Figure 14. The TOG peak was observed to be 33.2 ppm, the TOG average was 29 ppm, and the IAE was 1068. The peak of TOG was 0.9 ppm higher than that of the PI controller. In addition, an increase in IAE was observed.
Figure 14. Response of the TOG PD fuzzy control to the sinusoidal perturbation at the inlet flow rate

Source: The authors themselves.
The discarded water flow rate and the opening of the water discharge valve are shown in Figure 15.
Figure 15. Response of the discarded flow rate to the sinusoidal disturbance at the inlet flow rate

Source: The authors themselves.
Table 4 presents the results obtained in the simulation for each studied scenario. It can be verified that both controllers have satisfied legal requirements.
Table 4. Comparison between controllers

CONCLUSIONS
This work presented the modeling of a separation and treatment unit for produced water, consisting of a production separator and a battery of hydrocyclones. A mathematical model was developed for production separators whose input has high BSW and the water discharge rate is limited by the need to satisfy the minimum quality imposed by the legislation, which is a typical situation of production units operating in mature fields. It is proposed that the control of the discarded flow not be performed with the production separator interface control as is usually done, but rather be based on the TOG of the discarded water. In order for this control philosophy to be employed, the application of TOG meters is necessary. Thus, it is possible to optimize the process in real time, which is facilitated by Industry 4.0.
Both PI and Fuzzy PD controllers performed well and maintained the TOG of the discarded water within the legal requirements. The PI controller required less effort for parameter adjustment than the fuzzy PD. Notably, the fuzzy PD controller is usually tuned by trial-and-error, and a large number of simulations are necessary to obtain the pertinence functions that generated good control outputs. This fact may be related to the marginally lower result of this controller. Notably, such tests are difficult to perform on a real platform.
Based on the results, it is verifiable that one can apply a controller that regulates the flow of discarded water in a production separator with the control of the variable TOG. This controller can be deployed on separators whose water–oil interface control does not satisfy the needs of the process, requiring only the installation of an in-line TOG meter. Furthermore, the controller has the advantage of maximizing the flow of discarded water.
REFERENCES
Backi, C. J.; Brian A. G.; Skogestad, S. (2018), “A Control-and Estimation-Oriented Gravity Separator Model for Oil and Gas Applications Based upon First-Principles”, Industrial & Engineering Chemistry Research, Vol. 57, No. 21, pp. 7201-7217. Doi: 10.1021/acs.iecr.7b04297.
Brasil, N. I.; Araújo, M. A. S.; Sousa, E. C. M. (Organizadores) (2014), Processamento de Petróleo e Gás: petróleo e seus derivados, processamento primário, processos de refino, petroquímica, meio ambiente, 2 ed., LTC, Rio de Janeiro.
Castro, J. F.; Lima, C.; Gutierrez, R. (2015), “Projects and operations in the oil and gas E&P segment: a bibliographic panel”, Brazilian Journal of Operations & Production Management, Vol. 12, No. 2, pp. 306-320. https://doi.org/10.14488/BJOPM.2015.v12.n2.a10
Conselho Nacional de Meio Ambiente – CONAMA (2007), Resolução nº 393, de 8 de agosto de 2007, dispõe sobre o descarte contínuo de água de processo ou de produção em plataformas marítimas de petróleo e gás natural, e dá outras providências, available fom: http://www.mma.gov.br/port/conama/legiabre.cfm?codlegi=541. Accessed in Nov 01, 2017.
Farah, M. A. (2012), Petróleo e seus derivados: definição, constituição, aplicação, especificações, características de qualidade, LTC, Rio de Janeiro.
Filgueiras, N. G. T. (2005), Modelagem, análise e controle de um processo de separação óleo/água, dissertação de mestrado em Engenharia Química, Universidade Federal do Rio de Janeiro, Rio de Janeiro.
Kunert, R. (Ed.) (2007), Processamento primário de petróleo, Escola de Ciências e Tecnologias, Universidade Petrobras, Rio de Janeiro.
Lima, C. B. C.; Lima, G. B. A.; Quelhas, O. L. G.; Ferreira, R. N. (2015), “Integrated operations: value and approach in the oil industry”, Brazilian Journal of Operations & Production Management, Vol. 12, No. 1, pp. 74-87. https://doi.org/10.14488/BJOPM.2015.v12.n1.a8
Martins, F. B.; Cardoso, R.; Tammela, I.; Colombo, D.; Matos, B. A. (2018), “Applying CBM and PHM concepts with reliability approach for Blowout Preventer (BOP): a literature review”, Brazilian Journal of Operations & Production Management, Vol. 15, No. 1, pp. 78-95. https://doi.org/10.14488/BJOPM.2018.v15.n1.a8
Masoneilan International (2000), Masoneilan Control Valve Sizing Handbook, Dresser Valve Division, Bulletin OZ1000/00.
Nunes, G. C. (1194), Modelagem e simulação dinâmica de separador trifásico água-óleo-gás, dissertação de mestrado, Universidade Federal do Rio de Janeiro, Rio de Janeiro.
Nunes, G. C. (2001), Design and analysis of multivariable predictive control applied to an oil-water-gas separator: A polynomial approach (thesis), Division of Colleges & Universities, University of Florida, Florida.
Nunes, G. C. (2007), “Modelagem dinâmica do processamento primário de petróleo: conceitos fundamentais e aplicação em controle de processos”, Boletim Técnico da Produção de Petróleo, Vol. 2, No. 1.
Nunes, G. C.; Lima, E. L. (2006), Avaliação de diferentes estratégias de controle para hidrociclones para altos teores de óleo: relatório parcial, Petrobras, CENPES, Rio de Janeiro.
Nunes, G. C.; Medeiros, J. L.; Araújo O. Q. F. (2010), Modelagem e controle na produção de petróleo: aplicações em MATLAB, Blucher, São Paulo.
Othman, H. A.; Dabirian, R.; Gavrielatos, I.; Mohan, R.; Shoham, O. (2018), “Validation and improvement of the horizontal pipe separator model”, Society of Petrolium Engeneers, SPE Western Regional Meeting, 22-26 April, Garden Grove, California, USA. https://doi.org/10.2118/190047-MS
Paiva, V. W. M. M. C.; Copetti, A.; Bertini, L.; Campos, M. C. M. M.; Moratori, P. B. (2016), “Controle supervisório fuzzy aplicado ao processo de separação e tratamento de óleo e água em uma plataforma de petróleo”, XXI Congresso Brasileiro de Automática – CBA2016, Vitória - ES, 3-7 out., pp. 2187-2192.
Ribeiro, C. H. P. (2012), Controle preditivo multivariável com requisitos de qualidade em plataformas de produção de petróleo, dissertação de mestrado, Universidade Federal do Rio de Janeiro, Rio de Janeiro.
Ribeiro, C. H. P.; Miyoshi, S. C.; Secchi, A. R.; Bhaya, A. (2016), “Model Predictive Control with quality requirements on petroleum production platforms”, Journal of Petroleum Science and Engineering, Vol. 137, pp. 10–21. Doi: 10.1016/j.petrol.2015.11.004.
Silveira, M. A. C. R. (2006), Controle de um processo de tratamento primário de petróleo, dissertação de mestrado, Universidade Federal do Rio de Janeiro, Rio de Janeiro.
Stewart, M.; Arnold, K. (2008), Emulsions and oil treating equipment: Selection, sizing and troubleshooting, Elsevier.
Yayla, S.; Ibrahim, S. S.; Olcay, A. B. (2017), “Numerical investigation of coalescing plate system to understand the separation of water and oil in water treatment plant of petroleum industry”, Engineering Applications of Computational Fluid Mechanics, Vol. 11, No. 1, pp. 184-192. DOI: 10.1080/19942060.2016.1273137.
Received: 14 Dec 2018
Approved: 16 Apr 2019
DOI: 10.14488/BJOPM.2019.v16.n2.a15
How to cite: Nascimento, J. L.; Copetti, A.; Bertini, L. et al. (2019), “Evaluation of Total Oil and Grease with Flow Control for Mature Oil Fields in the Context of Industry 4.0”, Brazilian Journal of Operations & Production Management, Vol. 16, No. 2, pp. xxx, available from: https://bjopm.emnuvens.com.br/bjopm/article/view/663 (access year month day).