A Hybrid Ant Colony System and Tabu Search algorithm for the production planning of dynamic cellular manufacturing systems while confronting uncertain costs

Aidin Delgoshaei

delgoshaei.aidin@gmail.com

Kharazmi University, Tehran, Iran

Abolfazl Mirzazadeh

a.mirzazadeh@aut.ac.ir

Kharazmi University, Tehran, Iran

Ahad Ali

aali@ltu.edu

Lawrence Technological University, Michigan, United States of America

---

ABSTRACT

Highlights:

1. Cellular Manufacturing systems cover a wide range of industries.
2. Inflation rate can impose financial harms on cellular manufacturing systems.
3. The over-allocation of workers, which usually happens in dynamic systems, causes reduction of the system performance.
4. The proposed algorithm in this research can successfully schedule cellular systems to reduce system costs.

Goal:

The main aim is to determine the best trade-off values between in-house manufacturing and outsourcing, and track the impact of uncertain costs on gained schedules. To be more comprehensive, the performance of human resources is restricted and the partial demands are considered uncertain.

Design / Methodology / Approach:

In this paper a new method for minimizing human resource costs, including operating, salary, hiring, firing, and outsourcing in a dynamic cellular manufacturing system is presented where all system costs are uncertain during manufacturing periods and can be affected by inflation rate. For this purpose, a multi-period scheduling model that is flexible enough to use in real industries has been proposed. To solve the proposed model, a hybrid Ant Colony Optimization and the Tabu Search algorithm (ACTS) are proposed and the outcomes are compared with a Branch-and-Bound based algorithm.

Results:

Our findings showed that the inflation rate has significant effect on multi-period system planning. Moreover, utilizing system capability by the operator, for promoting and using temporary workers, can effectively reduce system costs. It is also found that workers’ performance has significant effect on total system costs.

Limitations of the investigation:

This research covers the cellular manufacturing systems.

Practical implications:

The algorithm is applied for 17 series of dataset that are found in the literature. The proposed algorithm can be easily applied in real industries.

Originality / Value:

The authors confirm that the current research and its results are original and have not been published before. The proposed algorithm is useful to schedule cellular manufacturing systems and analyse various production conditions.

Keywords: Human Resource Scheduling; Ant Colony Optimization; Skilled Worker Assigning; Out-Sourcing; Uncertain Costs.

---

1 INTRODUCTION

Designing Appropriate Facilities is vital for scheduling manufacturing systems engineering. Tompkins et al. (2003) reported that over $250 billion is estimated to be spent for facility designing, planning, and re-planning in the U.S every year. Material Transferring takes 20% to 50% of the total cost of manufacturing systems. An appropriate scheduling can reduce the mentioned costs by 10% to 30%. The Cellular manufacturing system (CMS) is a trustful way of using group technology. In a cellular system, the layout is designed in a way as to use the advantages of manufacturing flexibility and efficient flow by grouping machines according to the families of products (Papaioannou and Wilson, 2010). Human resource management (HRM) is considered an important issue in CMS problems through the last 3 decades. During the year 2013, U.S. spent $7.0 billion for training and employment programs. Hence, during last decades, scientists made their best efforts to define and solve HRM problems in different circumstances, conditions and situations to find out new ways to reduce such expenses.

Perhaps, determining the optimal number of workers in different cells is the main idea of HRM problems in CMS. In 1994, Morris and Tersine simulated some cell layouts by considering equipment and labor (Morris and Tersine, 1994). Next year, to determine the optimal number of operators and assigning them to parts, Park and Lee (1995) developed a 2-stage model while in the first stage, a Taguchi method was used to determine a system performance that was then used as the objective function of the assigning model. The idea of maximizing saving costs between operating and outsourcing was investigated by Heady (1997). But their model did not investigate operator level, training, hiring and firing costs. Afterward, Norman et al. (2002) focused on assigning workers in CMS when the aim was maximizing system profit and then Ertay and Ruan (2005) developed the idea of determining the number of operators to optimize the number of output products. For this purpose, using weighted input data, a data envelopment analysis (DEA) was applied. But they failed to consider skill levels of the operators and machines.

The idea of considering operator levels was developed by Suer and Cedeño (1996). For this purpose, a mixed integer programming method was used to generate alternative operator levels and then an integer programming method was used to find the optimal operator assignments in cells. The idea of worker assigning and training problem in functional and cellular layouts was then followed by R. G. Askin & Huang (1997). In addition, Aryanezhad et al. (2009) considered three skill levels for workers, which can be promoted through the planning horizon by training, in a multi period scheduling model, for simultaneous cell forming and worker assignning.

As a different point of view, R. Askin and Huang (2001) studied the performance of heuristics as the greedy algorithm and the simulated annealing algorithm for creating team works and promoting teams, using cross-training plan in CMS. Slomp and Suresh (2005) focused on assigining workers to team works with the aim of minimizing the training and assigning costs while maximizing labor flexibility. In the same year, Fitzpatrick and Askin (2005) argued that elements of a good team formation are not only limited to personal skills and characteristics but also technological and human interactions. Hence, using pre-determined skill level measures, they tried to select workers and assign them to appropriate teams in cells to maximize team performance. At the same time, Cesaní and Steudel (2005) focused on work sharing, work balancing and leveling the operator assignments in the presence of bottleneck operations. For continuing to prevent over loading and over assigning, Satoglu and Suresh (2009) used goal programming method in a mathematical model, where the objectives were minimizing over assignment of workers, cross training, hiring, and firing costs.

Cross-trained workers are referred to those workers that trained to perform more than one task. By determining the best set of cross-training, workers can improve system performance. In 1996, Bartholdi and Eisenstein declared that, considering larger cells that are equipped with multi-skilled workers and various workstations causes a more stable work place, thus yielding emerging balanced production lines and maximizing production volume as well (Bartholdi & Eisenstein, 1996). Afterward, Kleiner et al. (1998) took charge of skilled workers, in a computer-based system. The proposed system that was employed in an air craft component manufacturing company in U.S included cell lead time, part travel distance, process yield, operator classification, and labor efficiency. In continue, it was proved that cross-trained workers can achieve higher performance than normal workers (Gel et al., 2000) and top management role and cross-trained employees have significant impact on the successful implementation of CMS (Olorunniwo and Udo, 2002). In the year 2000, Kher found that by using cross-trained attributions, such as learning and re-learning, more effective training schemes can be provided (Kher, 2000). The idea of distributing skilled workers within teams and the degree of the workforce belongs to Molleman and Slomp (1999), where they indicated that such items have important effects on the performance of CMS. They showed that using appropriate plans to promote and distribute skilled workers yields remarkable results on the performance of the system and, as a result, each of the workers will be an expert in more than one skill. Later, four cross-training policies, which were considered based on workload of the bottleneck workers in certain and uncertain work conditions, were compared by Slomp and Molleman (2002). The results confirmed that better team performance can be expected by using higher levels of cross-training workers. Then, the staffing level and shop layouts in the department, strictly and hybrid cell layouts were taken into consideration (Jensen, 2000), by changing the number of employees in each department and considering three levels of workload balance and two labor transferring rules. Jensen evaluated product flow and job tardiness. Recently, Li et al. (2012) focused on minimizing average salary while maximizing average of satisfaction. For this purpose they developed a multi-objective mixed integer programming method to determine the number of cross-trained labors and also tasks that must be assigned to the labors in flexible assembly cell layout. Another contribution of their research was considering worker satisfaction and task redundancy levels.

Recently, the idea of considering dynamic part demands in HRM-CMS, which can cause system imbalance, is more popular, as it was less developed before. To solve this problem, Mahdavi et al. (2010) developed a multi-mode planning method aiming at workers’ assignments in a reconfigurable CMS. In the proposed model, hiring, firing, and also salary costs were considered as a part of total system costs. They also considered the available time for workers. Afterward, they focused on inter-cellular movements of workers and parts while processing on a specific machine (Mahdavi et al., 2012). The contribution of this study was adding workers as the 3rd dimension of machine-part incidence matrix by using a cubic matrix.

Delgoshaei et al. (2016b) reviewed material transferring models and approaches and illustrated the drawbacks emerged while transferring materials in CMS. In the same year, Delgoshaei et al. (2016a) proposed a new method for reducing the cell load variation in dynamic CMS. Delgoshaei et al. (2017) used a hybrid genetic algorithm and simulated annealing for scheduling CMS.

An in-depth survey in the history of HRM problems in CMS (Table 1) shows the trade-off issue between in-house manufacturing, considering the skilled workers, the hiring and firing of temporary workers, and outsourcing, while part of the demands are considered uncertain and human performance is not fixed and is less developed. Moreover, system costs are considered fixed while in the real world, system costs shall not be considered equal in different time intervals, as they may be affected by many factors, such as inflation rate (Delgoshaei et al., 2014). In this research, a new mixed integer mathematical model is addressed by considering uncertain costs to find the best combination of worker allocation and outsourcing in the presence of the mentioned condition.

Table 1. Comparing the opted researches from the literature

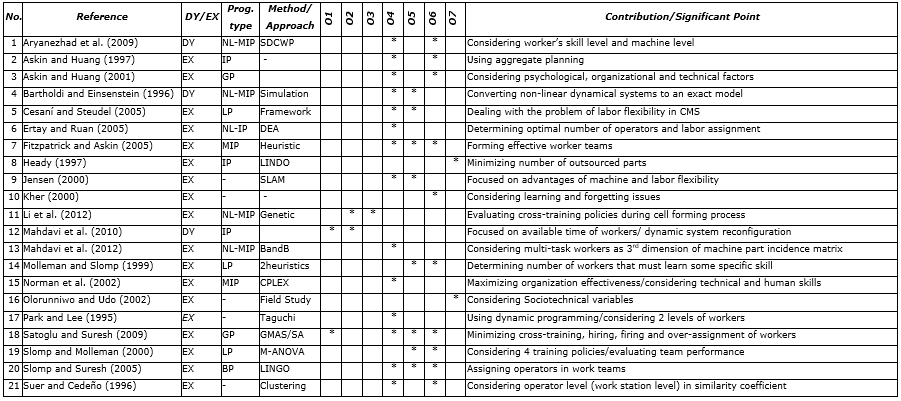
DY/EX - Dynamic/Exact; Prog. type - Programming type; LP - Linear Programming; DP - Dynamic Programming; IP - Integer Programming; NL-MIP -Non-linear Mixed Integer Programming; GP - Goal; O1 Hiring and Firing; O2 - Worker Satisfaction; O3 - Salary; O4 - Worker Assignment; O5 - Labor Efficiency; O6 - Training/Skill level; O7 - Outsourcing.

2 THE PROPOSED MODEL

In this section a framework is used to examine the performance of the model. The framework has steps to provide production plans by using skilled workers, hiring and firing temporary workers (as needed) and outsourcing respectively is developed (Figure 1). In many real cases managers may prefer in-house manufacturing than outsourcing since outsourcing may be more costly or may cause some quality problems or on-time producing. Despite, in some cases, others may desire to use outsource services due to use suppliers that provide cheaper parts in a reasonable quality or lack of technology. In this study the main reason for using outsource services is the lack of enough system capacity for fulfilling demands in a specific period. For this purpose, the proposed framework is prepared to balance the in-house capacity periodically based on customer demands promoting workers and/or hiring temporary workers before using subcontractor’s services (as needed). Hence, the steps of the method are designed as:

1. Generating initial layout (using initial sets of workers to cells).
2. Promoting workers by improving skills of the fixed operators using training budget.
3. Hiring new temporary workers for fulfilling the remained part demands.
4. Firing extra temporary workers to reduce system costs (if exists).
5. Using outsource services if any part demands are still remains.

Figure 1. Flowchart of the proposed framework

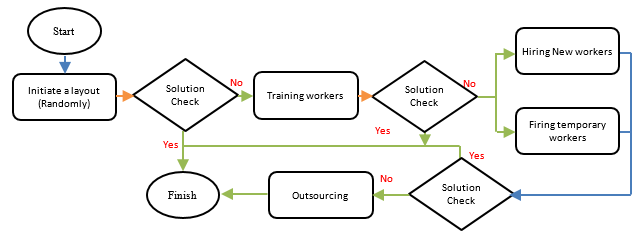
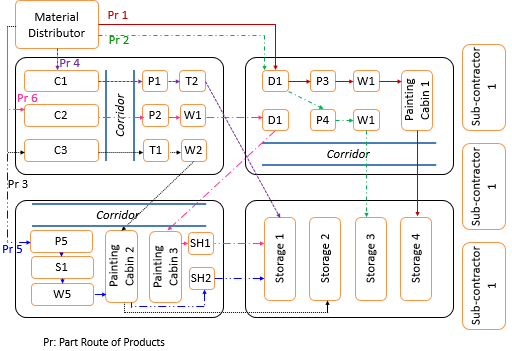
After generating initial layouts by using forward serial programming, the main strategy is to satisfy customer needs by promoting fixed operators (current workers) before hiring new ones. If promoting available workers in any planning period can cover the customer needs, there will be no need to hire temporary workers or to use outsource services which is mostly expensive. Otherwise, with respect to cell sizes, the algorithm focuses on hiring new workers that will be considered as temporary workers. Note that cell size can be controlled by lower and upper cell boundaries through the planning horizon. Such workers are considered temporary since they are temporarily hired to fulfill the customer demands in a planning slot. Therefore they are not eligible for further training unless the algorithm decided to keep them for another planning period. In continue, if the maximum capability of in-door manufacturing is impotent to satisfy the customer needs, using the services of collaborating firms or subcontractors will be suggested. The explained logic will be kept in the solving process of all metaheuristics that will be deigned in the next part. Figure 2 shows a typical layout of CMS where part demands are manufactured using the system capacity and the rest of those parts that cannot be completely manufactured inside the system are planned to allocate to subcontractors.

Figure 2. A Flow Diagram of Work Assigning and Outsourcing in a Cellular Manufacturing System

The following items show the assumptions that are taken into consideration in order to provide production plan alternatives by means of system capability and also outsource services:

1. Maximum number of cells is fixed through the planning horizon.
2. Maximum and minimum numbers of workers that can be allocated to each cell are controlled using upper and lower boundaries.
3. The performance of fixed operators and temporary workers is not constant and will be affected by increasing the volume of production.
4. Inflation rate is not constant and, hence, all system costs will be changed periodically through planning horizon.
5. Part demands are not fixed and supposed to change periodically. Part demands will be calculated using normal function distribution.
6. Promoting Workers is allowed through planning horizon.
7. Training which is done to promote workers takes no time and the training cost for each skill level is known in advance.
8. The skill level and skill-production rate coefficients are fixed and known in advance.
9. In firing condition, swapping fixed operators is prohibited unless there was no temporary worker.
10. Each location can be filled by only one worker.

2.1 Inputs

i: number of parts

k: number of cells

s: types of operators

f: number of operators

n: number of skills

t: planning periods (time slots)

Sc: size of cells

2.2 Parameters

2.3 Matrixes

Number of operators that are available at the beginning of planning period (NOP_s) [⋱]_s

Operator-Part incidence: Ability of the operator type S in manufacturing part i (OPI_i,s) [⋱]_is

Operator-Part ability incidence: Ability of manufacturing part i while the skill level of the operator is n (OPAI_i,n) [⋱]_iXn

2.4 Variables

2.5 Mathematical Model

The proposing model can be developed now as a non-linear mixed integer programming method:

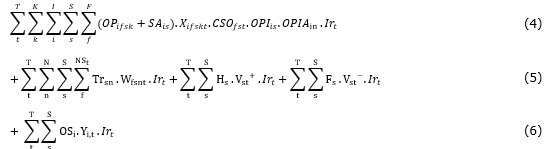
The first sentence in the objective function is developed to show the operating cost including machinery and wage of processing of each part. The second sentence explains the training costs that will be applicable only for fixed operators. The third and fourth sentences show hiring and firing temporary workers respectively and the final sentence of objective function is used for determining outsource values. The inflation rate affects the different types of system costs in the model. This will allow the decision makers to analyze the role of uncertain costs in increasing system entropy.

The first series of constraints are used for assuring that each of the products will be produced not less than its market demand (whether inside the company or using outsource services) through planning slots. The second constraint allows managers to pre-determine the proportion of producing products in the system or using outsource services based on the company policies. The third constraint controls promoting worker’s skill according to the training budget in each planning slot. The fourth constraint ensures that the number of workers (whether temporary or fixed) will change logically in each period. The fifth constraint sets the initial number of each worker types in the first period. The sixth constraint is used to guarantee that the number of workers in each planning slot will not exceed or be less than the upper and lower bounds, respectively. The seventh constraint ensures that none of the workers will be assigned more than his/her capability. The next three sets of constraints are designed to set initial worker’s skills and to make sure that the skill levels will not increase infinitely. The rest of the constraints is used to control the domain of the variables.

2.6 Solution representing

In both solving methods, which will be explained next, the scheme of representing the solutions of the model is illustrated by developing a solution-string that contains four matrixes where the 1st matrix shows positions of operators in cell layout, the second matrix indicates the skill level of each operator, the third matrix reveals the amount of assigned parts to each operator and the last matrix shows the amount of each part types that decided to be processed by subcontractors (Figure 3).

Figure 3. A representing scheme sample

The degree of hardness of the proposed model is (n^s)^k.UL. Hence, for example, for a small size problem (suppose 5 cells with the capacity of 8 operators in each cell, 4 operator types and 3 skill levels), the number of possible solutions (both feasible and non-feasible) can be calculated as:

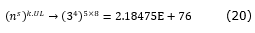
As mentioned by Fitzpatrick and Askin (2005) even small size problems in such cases are hard to solve using normal optimizing algorithms. Hence, in next part, a typical branch and bound algorithm (BandB) is developed and then propose an ACS that is strengthened using the positive features of tabu search algorithm is proposed. Then, the results of the BandB and ACS will be compared.

3 SOLVING ALGORITHMS

3.1 Branch and Bound Algorithm

Branch and bound algorithm is generally employed to find optimal solutions in optimization problems where all new solutions are compared with a lower or upper (or both) bounds. BandB can be designed as a single or multi start-point algorithm and the number of neighbors for each iteration may be varied (based on solution string), which helps to search solution spaces more comprehensively, but at the same time BandB is not applicable for continuous variable models in its classic form since it was designed for solving discrete variable problems. In addition, one big drawback with BandB is the lack of a mechanism for escaping from local optima. Hence, BandB is more sensitive for falling into local optima. Moreover, although BandB is a fast tracking and reliable algorithm for small and medium scale problems, for large scale and complicated problems, BandB is more risky to encounter with the “early stage convergence” phenomenon.

3.1.1 Choosing number of neighbors

The proposed algorithm uses the replacing strategy for generating new feasible solutions (Figure 4). It is noted that various strategies are available for searching neighbors of a solution that must be chosen based on the nature and circumstances of each problem. Replacing elements, improving an element or zero-one shifting are among popular methods. In this case, such elements are defined by replacing workers with different work skills.

Suppose as an initial solution:

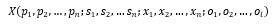
Then,

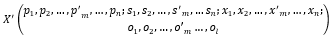is a new neighbor that can be generated by shifting the m^th element in the initial solution.

Figure 4. Choosing a new feasible neighbor in B&B algorithm

3.1.2 Objective function operator

The objective function of the proposed mathematical model is considered the main operator for evaluating the new neighbors:

In the next step, using the following formula, the best neighbor for each solution (say ‘r’) will be chosen:

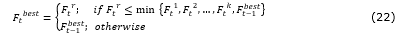
Table 2. Pseudo code for the BandB algorithm

3.1.3 Terminating criteria

1. If maximum number of iteration is reached.

2. If there is no further opportunity for improvement:

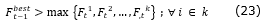
The equation above means that the searching process will be terminated if none of the generated solutions in the current iteration is better than pervious stages so that no improvement will be expected (Figure 5). Note that such status will occur as a consequence of achieving optimum solution or encountering with a local optimum. Choosing improper number of neighbors (k) is another reason that may cause the algorithm to be impotent.

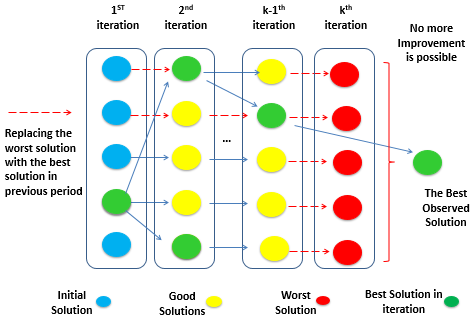
Figure 5. Solving Process Scheme of B&B algorithm, considering one neighbor for each solution

3.2 The Hybrid Ant Colony Optimization and Tabu Search (ACTS)

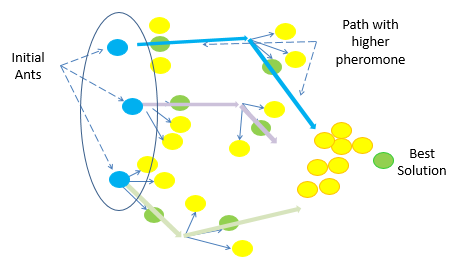
Ant colony optimization is inspired from the swarm intelligence of real ants that live in big colonies (hundred thousand of ants). As an optimizing method, it was firstly used by Dorigo (1992) and a few years later it was recognized among well reputed metaheuristics. The main aim of the classic version of ACO, which was designed to solve discrete optimization problems, was to find a smaller path in a graph, but other versions were promoted to solve continuous problems with various objectives. Figure 6 shows how ACO finds the path with minimum distance (as an objective function).

Figure 6. Solving Process Scheme of Ant Colony

3.2.1 Initial Colony Size and Pheromone Update

Choosing an appropriate number of colony members plays a key role in providing better solutions in Ant colony systems. But at the same time, choosing big size of colony members causes more computations and more computation time accordingly. Each colony member is a representative of a solution string that has the opportunity of development in next iteration. While a new neighbor is generated, the efficiency of the new path will be evaluated by calculating the value of the sprinkled pheromone using the formula below:

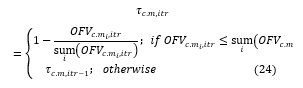
The above formula uses the amount of objective function value (total system costs) as the main operator for calculating the amount of pheromone sprinkle of each colony member. Therefore, the more objective function value saving occurs in a path, the more pheromone will be sprinkled. Otherwise, the best amount among pheromones in the last iteration will be considered for the colony member that provide a chance for worse solution to stay in an optimizing process for the next iterations and does not throw them away instantly. Such strategy is suitable for escaping from local optimum.

3.2.2 Evaporating Pheromones

ACO has a powerful improving engine that enables it for providing good solutions, but at the same time, such improving speed increases the speed of solution convergence. To prevent it, three different strategies can be used:

1. Choosing larger sets of colony members that increase computation time as well.

2. Using a list of solutions with higher pheromones: considering only one member (with the highest pheromone level) in iteration as a candidate for the rest of optimizing process causes immediate elimination of the other colony members. Therefore, the algorithm should not consider the best pheromone as the only candidate for the next iteration, but instead a probability function will be used to create a tournament list of better pheromones in a way that colony members with higher pheromone have more chance to be chosen for the rest of the optimization process. Such strategy also prevents early stage convergence and helps to escape local optimum traps:

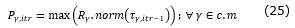
R is a uniformed random number between 0 and 1. The above formula chooses a value among normalized pheromones that are sorted in an ascending way. It is obvious that members with higher values have more chance to be chosen.

3. Using short-term and long-term memories as what was used in the Tabu search algorithm: Due to high capability of Tabu search for finding solutions in Np-hard problems, which comes as a consequence of using memories (short-term and long-term), TS has been widely used as part of a hybrid with other algorithms. Roux et al. (1999) developed a hybrid Ant System (AS) and TS called ANTabu to solve optimization problems. A few years later, Kaji (2001) also employed the hybrid of AS and TS for solving travelling salesman problem.

In this study the mechanism of short-term and long-term memories of TS was used as a part of searching process in ACO.The logic of TS is based on using short-term memory to prohibit revisiting those solutions that had been rejected before and also those whom are banned by the algorithm for some reason (long-term memory).

Figure 7. Solving Process Scheme of Tabu Search

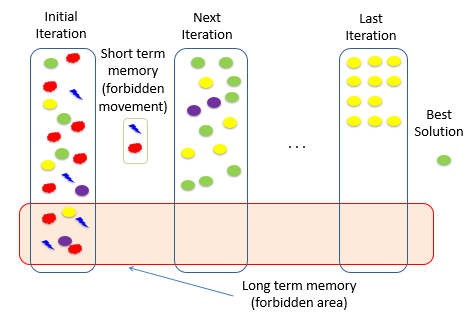
In 1986, Glover developed TS to overcome defects of searching neighborhood spaces (Glover, 1986). Tabu search is an effective way of local searching technique that improves the chances of finding optimum or near optimum solutions by defining such memory structures in a way that, if a potential solution has been rejected in a certain period before or if it violates a rule, it will be marked as a "tabu" (forbidden) movement so that the algorithm will not consider it for a certain period in next iterations (Figure 7).

3.2.3 Intensification

During the process of searching local neighbors, the algorithm may encounter a lot of elite neighbours. In such condition, it is better to have a mechanism for increasing the search for the number of neighbors for a short time. Using such strategy helps providing a good structure for concentrating more comprehensively on elite members in local areas. An appropriate short-term memory, provides an effective way for searching elites in local areas as it prevents searching worse elements (Figure 7).

3.2.4 Diversification

Diversification is another common problem that emerges while using TS algorithm. As mentioned before, TS algorithm works based on functions that prohibit searching the areas in a solution space that has been searched before with no sign of improvements. To prevent such problem, two strategies are considered:

Proposition 1: The first strategy is using capacity restricted long-term memory with the ability of updating during iterations. Through the use of such strategy a new candidate will be replaced with the oldest member of long-term memory whenever the long-term memory is full.

Proof: Imagine an initial allocation of workers that are eligible to develop by training, hiring (or firing) and outsourcing in a layout. If using an initial distribution of workers for providing the next neighbors causes worse objective function, then this cell layout will be considered a member of long-term memory:

Proposition 2: Using inspiration rate helps to fade old members of the tabu list. Hence, if an area is banned in an iteration, it will not last until the end of the searching process, but instead, after a period (even if the Tabu list is not updated), the older members will be faded one by one. Through the use of such strategy the areas that have been forbidden in the early stages of the solving process will have a chance to be involved in later iteratations again, thus helping to prevent early stage solution convergence.

Proof:

3.2.5 Short-term Memory

Proposition: In this study short-term memory is considered during training procedure in a way that, if promoting an operator (in a specific planning slot) causes less production volume than outsourcing, this level of training is banned temporarily for that operator until the following planning slot.

Proof:

3.2.6 Long-term Memory

Proposition: As mentioned before, the framework starts by generating initial ants (cell layouts) randomly, which are then promoted using training, hiring and using outsource services. Suppose that, after preparing a solution, if the objective function of an ant is worse than all other colony members in previous iterations, it means that this cell layout is not a good candidate for improvement. In such condition, there is no need to focus on the mentioned area. Hence, the initial layout that was generated during the first step of the framework is forbidden for the coming iteration.

Proof:

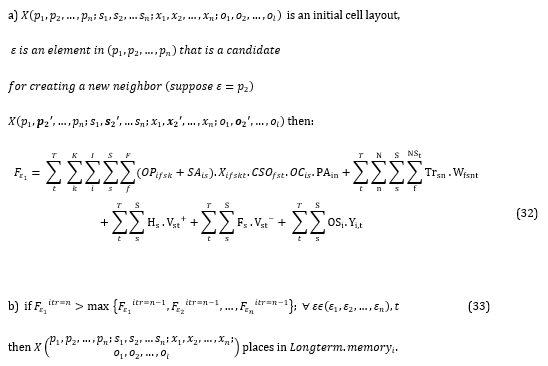
3.3 Parameter Setup

Since metaheuristics are sensitive to initial parameter settings, it is important to use appropriate parameters, otherwise the quality of results may not be good enough (Delgoshaei et al., 2014). The number of iterations for BandB and ACTS is set depending on the size of the problem (150, 200, and 250 for small, medium and large size problems, respectively). The same strategy is used for determining the number of neighborhood sizes, where 150, 200, and 250 neighbors are considered for BandB and ACTS. Since the chance of encountering with local optima are varied from each case to another, three different evaporation rates are supposed for ACTS (0o.1, 0.3, and 0.5) and similar rates are considered as local escaping rate. For ACTS, the Tabu list size is supposed to change based on the scale of problems (2, 3, and 5).

In order to minimize the effects of using estimated parameters (such as number of colony members, iterations, and tabu list size) for the proposed algorithm, a similar way that was used by Li et al. (2012), where they solve all experimented ten times, was followed.

4 EXPERIMENTS AND RESULTS

To examine and evaluate the performance of the proposed ACTS algorithm for the proposed method, a number of experiments from the literature is solved (Table 3). All examples were solved by BandB and ACTS using Matlab® R2009 software, which is installed on a Core™ i7 personal laptop that was supported by 2.40 GH CPU and 8 GB RAM.

Table 3. Table of Input Data for Experiments that were gathered from the literature*

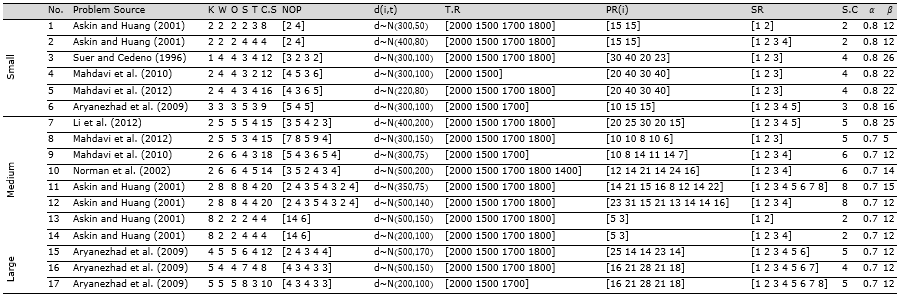
K: Cell Number; W: Number of Workers; O: Number of Operations; S: Skill Level; T: Time Slots; C.S: Cell Size; NOP: Initial Number of Operators; d(i,t): Part Demands; T.R: Training Budget; PR(i): Production rate; SR: Skill rate; SC: Number of sub-contractors.

*While gathering data in each case, the authors tried to use applicable data. It is noted that other required parameters are generated by the members of this research.

4.1 Discussion

Results showed that in a certain number of iteration, in 47.06% of the solved cases, ACTS provided better solutions by escaping from local optima and in 29.01% both algorithms reported the same results (Table 4). The main reason for such improvement is the use of short- and long-term memories that enable ACTS to provide better solutions in the same number of iterations (up to 2.24%).

Although in most of the cases, the average of the schedules that was achieved by using ACTS causes smaller system costs in a specific number of program repetition, at the same time, ACTS consumes more computations and needs more time accordingly. Besides, comparing the variance between the results of both methods shows that the value of improvements is varied for different problems and depends on the structure of problems; hence, it cannot be predicted in advance. The results also show that, while large scale problems are taken into account, ACTS provides better solutions most of the times (Figure 6). Such results reveal the importance of using an effective structure for escaping from local optima in ACTS. Although the increase in the number of solutions in iterations and in the number of neighborhoods can strengthen the possibility of escaping from the local optima, ACTS can provide still better schedules in the specific number of iterations. In addition, it was found that the speed of convergence in BandB is faster than ACTS.

Table 4. Results of solving the experiments gathered from the literature

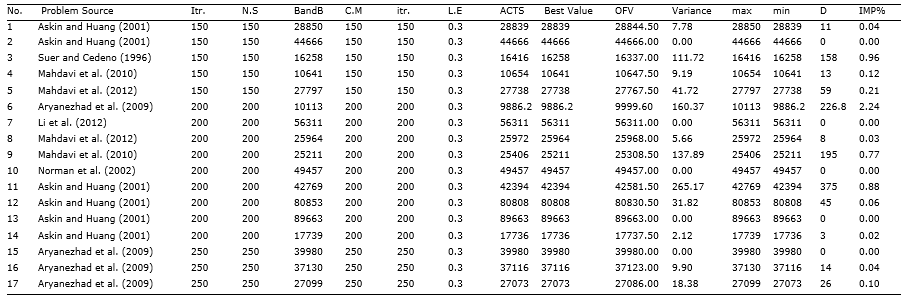
Itr. - Iteration; N.S - Neighbourhood Size; IMP% - Improvements Percentage

It is figured out that the proposed framework can effectively improve the objective function by reducing system costs. Such improvement is a result of finding the best values of appointing skilled operators, temporary workers (hiring and firing) and subcontractor’s services. Results clear that inflation rate and operator performances are two important factors that can affect system performance in cellular manufacturing systems. To evaluate the impact of inflation rate on system costs, all problems are solved, again considering two assumptions. In the first case, all system costs are considered fixed during planning horizon, while in the other status, system costs are uncertain and are supposed to be changed periodically (Table 5). It is found that increasing inflation rate causes increasing system costs and will change the balance of schedules (in terms of indoor manufacturing and using outsource services).

Table 5. Comparing Results of ACTS, Considering Fixed and Uncertain Costs

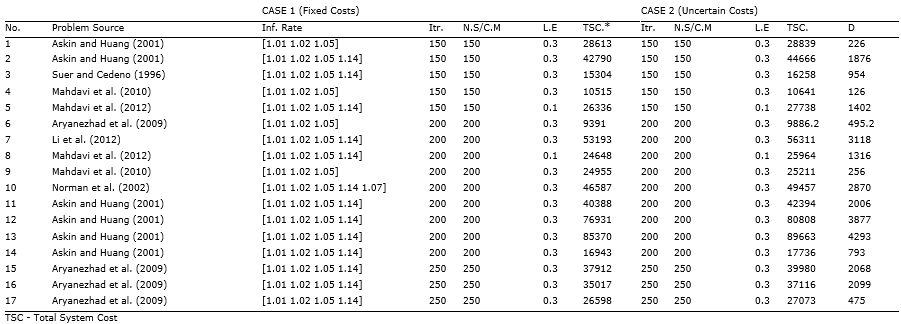
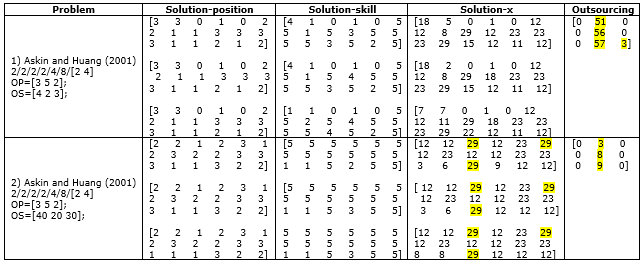
Moreover, while using subcontractor services is more expensive or whenever the total the effective capacity of a company is not used, the framework tends to use in-house manufacturing by improving fixed operator’s skills or hiring new temporary workers. Although such scenario leads reducing system costs, the operators may become over-allocated. In contrast, if using the outsource services is cheaper than in-door manufacturing, the system may become too dependent on the use of outdoor services. Table 6 compares the results of solving a problem, where all the settings and conditions are equal except for the outsourcing price. In the first cast, the outsourcing price is too low and close to the in-house manufacturing, which cause system to be more dependent on outsource services in the period of the planning horizon (see the right column of the table 6). In contrast, in the second case, the out sourcing costs are considered too much. As a result, the algorithm decided to produce more in-house parts that cause operators over-allocating. It is also found that the possibility of increasing system costs as a cause of mismatching between worker’s promoting and outsourcing is increased in the dynamic condition of market.

Table 6. The system is too dependent on outsource services (Problem 1) / Operators are over-allocated (Problem 2)

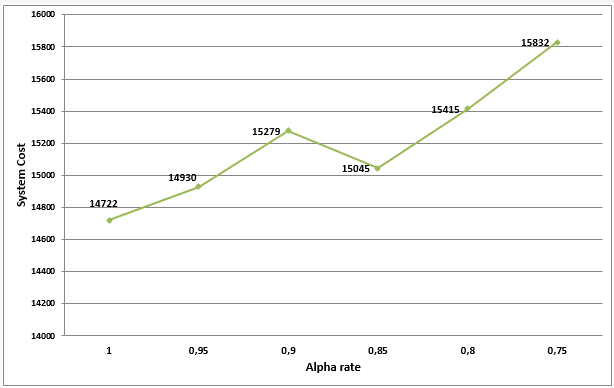
As mentioned before, the performance rate of operators is another factor that can influence the scheduling of a system and system costs, accordingly. Figure 8 indicates different costs of a system where all other settings are considered the same; however, different performance rates are taken into consideration. The positive slope of the trend line shows that, while the performance rate of workers is decreased, the total system cost increases. Such phenomenon happens as a result of decreasing the production volume of the system that causes an increase in the amount of outsourcing accordingly.

Figure 8. Trend line shows increase system cost, while decreasing performance rate

4.2 Performance Metric for Evaluating Results

Finding suitable metrics that can provide a base for comparing results is essential. For this manner, a formula is developed to check the amount of reducing total system cost, comparing with the average of results that was achieved by both algorithms.

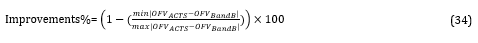
The formula above shows how better ACTS can reduce total system costs compared to the other algorithm. Table 4 shows that the performance of ACTS in most of the cases is better than BandB (up to 2.24%), which means that comparing with BandB, ACTS can improve the system costs more effectively.

5 CONCLUSION

In this research, a new programming method is proposed to assign skilled operators and temporary workers and use subcontractors’ services in cellular manufacturing systems. Then the impact of uncertain costs and operator’s performance on dynamic cellular manufacturing systems is evaluated. The developed problem (as it was found for many similar problems in the literature) is sensitive to model dimension and therefore the developed model is an NP-hard problem. To overcome such shortcoming, a hybrid ACO and TS algorithms is developed. It is observed that inflation rate has negative effects on the scheduling of cellular manufacturing systems. Over-allocating workers and creating reliant systems (on subcontractors) are two events that emerge as a consequence of the increasing inflation rate. Over-allocating workers that usually happens in dynamic systems causes reduction of the system performance that can significantly affect production schedules and increase the total system costs. It is also found that, while partial demands are uncertain, finding the best quota of manufacturing production and using outsource services is vital and can significantly improve the system productivity by reducing system costs. In this manner, hiring or firing temporary workers (as needed) and promoting skilled workers play a key role. Future research in this area is suggested by considering different payment methods for both skilled workers and subcontractors.

Acknowledgements

The authors would like to sincerely appreciate the editorial team and also anonymous reviewers for their positive and constructive comments which are used to improve the manuscript.

---

6 REFERENCES

Aryanezhad, M.; Deljoo, V.; Mirzapour Al-e-hashem, S. (2009), "Dynamic cell formation and the worker assignment problem: a new model", The International Journal of Advanced Manufacturing Technology. Vol. 41. No. 3-4, pp. 329-342.

Askin, R.; Huang, Y. (2001), "Forming effective worker teams for cellular manufacturing", International Journal of Production Research. Vol. 39. No. 11, pp. 2431-2451.

Askin, R. G.; Huang, Y. (1997), "Employee training and assignment for facility reconfiguration", Proceedings of the 1997 6th Annual Industrial Engineering Research Conference, IERC, Miami, FL. 426-431.

Bartholdi, J. J.; Eisenstein, D. D. (1996), "A production line that balances itself", Operations Research. Vol. 44. No. 1, pp. 21-34.

Cesaní, V. I.; Steudel, H. J. (2005), "A study of labor assignment flexibility in cellular manufacturing systems", Computers & industrial engineering. Vol. 48. No. 3, pp. 571-591.

Delgoshaei, A.; Ariffin, M.; Baharudin, B.; Leman, Z. (2016a), "A new method for decreasing cell-load variation in dynamic cellular manufacturing systems", International Journal of Industrial Engineering Computations. Vol. 7. No. 1, pp. 83-110.

Delgoshaei, A.; Ariffin, M. K.; Baharudin, B. H. T. B.; Leman, Z. (2014), "A Backward Approach for Maximizing Net Present Value of Multi-mode Pre-emptive Resource-Constrained Project Scheduling Problem with Discounted Cash Flows Using Simulated Annealing Algorithm", International Journal of Industrial Engineering and Management. Vol. 5. No. 3, pp. 151-158.

Delgoshaei, A.; Ariffin, M. K. A.; Ali, A. (2017), "A multi-period scheduling method for trading-off between skilled-workers allocation and outsource service usage in dynamic CMS", International Journal of Production Research. Vol. 55. No. 4, pp. 997-1039.

Delgoshaei, A.; Ariffin, M. K. A. M.; Leman, Z.; Baharudin, B. H. T. B.; Gomes, C. (2016b), "Review of evolution of cellular manufacturing system’s approaches: Material transferring models", International Journal of Precision Engineering and Manufacturing. Vol. 17. No. 1, pp. 131-149.

Dorigo, M. (1992), Optimization, learning and natural algorithms, PhD Thesis, Politecnico di Milano, Italy.

Ertay, T.; Ruan, D. (2005), "Data envelopment analysis based decision model for optimal operator allocation in CMS", European Journal of Operational Research. Vol. 164. No. 3, pp. 800-810.

Fitzpatrick, E. L.; Askin, R. G. (2005), "Forming effective worker teams with multi-functional skill requirements", Computers & industrial engineering. Vol. 48. No. 3, pp. 593-608.

Gel, E.; Hopp, W.; Van Oyen, M. (2000), Workforce agility in systems with hierarchical cross-training: working paper, Northwestern University Evanston, IL.

Glover, F. (1986), "Future paths for integer programming and links to artificial intelligence", Computers & Operations Research. Vol. 13. No. 5, pp. 533-549.

Heady, R. B. (1997), "Forming minimum-cost machine cells with exceptional parts using zero-one integer programming", Journal of Manufacturing Systems. Vol. 16. No. 2, pp. 79-90.

Jensen, J. B. (2000), "The impact of resource flexibility and staffing decisions on cellular and departmental shop performance", European Journal of Operational Research. Vol. 127. No. 2, pp. 279-296.

Kaji, T. (2001), "Approach by ant tabu agents for Traveling Salesman Problem", Systems, Man, and Cybernetics, 2001 IEEE International Conference on. 3429-3434.

Kher, H. V. (2000), "Examination of flexibility acquisition policies in dual resource constrained job shops with simultaneous worker learning and forgetting effects", Journal of the Operational Research Society. Vol. No., pp. 592-601.

Kleiner, B. M.; Drury, C. G.; Palepu, P. (1998), "A computer-based productivity and quality management system for cellular manufacturing", Computers & industrial engineering. Vol. 34. No. 1, pp. 207-217.

Li, Q.; Gong, J.; Fung, R. Y.; Tang, J. (2012), "Multi-objective optimal cross-training configuration models for an assembly cell using non-dominated sorting genetic algorithm-II", International Journal of Computer Integrated Manufacturing. Vol. 25. No. 11, pp. 981-995.

Mahdavi, I.; Aalaei, A.; Paydar, M. M.; Solimanpur, M. (2010), "Designing a mathematical model for dynamic cellular manufacturing systems considering production planning and worker assignment", Computers & Mathematics with Applications. Vol. 60. No. 4, pp. 1014-1025.

Mahdavi, I.; Aalaei, A.; Paydar, M. M.; Solimanpur, M. (2012), "A new mathematical model for integrating all incidence matrices in multi-dimensional cellular manufacturing system", Journal of Manufacturing Systems. Vol. 31. No. 2, pp. 214-223.

Molleman, E.; Slomp, J. (1999), "Functional flexibility and team performance", International Journal of Production Research. Vol. 37. No. 8, pp. 1837-1858.

Morris, J. S.; Tersine, R. J. (1994), "A simulation comparison of process and cellular layouts in a dual resource constrained environment", Computers & industrial engineering. Vol. 26. No. 4, pp. 733-741.

Norman, B. A.; Tharmmaphornphilas, W.; Needy, K. L.; Bidanda, B.; Warner, R. C. (2002), "Worker assignment in cellular manufacturing considering technical and human skills", International Journal of Production Research. Vol. 40. No. 6, pp. 1479-1492.

Olorunniwo, F.; Udo, G. (2002), "The impact of management and employees on cellular manufacturing implementation", International Journal of Production Economics. Vol. 76. No. 1, pp. 27-38.

Papaioannou, G.; Wilson, J. M. (2010), "The evolution of cell formation problem methodologies based on recent studies (1997–2008): Review and directions for future research", European Journal of Operational Research. Vol. 206. No. 3, pp. 509-521.

Park, T.; Lee, H. (1995), "Design of a manufacturing cell in consideration of multiple objective performance measures", Manufacturing research and technology. Vol. 24. No., pp. 181-202.

Roux, O.; Fonlupt, C.; Talbi, E.-G.; Robilliard, D. (1999), ANTabu--enhanced version.

Satoglu, S. I.; Suresh, N. C. (2009), "A goal-programming approach for design of hybrid cellular manufacturing systems in dual resource constrained environments", Computers & industrial engineering. Vol. 56. No. 2, pp. 560-575.

Slomp, J.; Molleman, E. (2002), "Cross-training policies and team performance", International Journal of Production Research. Vol. 40. No. 5, pp. 1193-1219.

Slomp, J.; Suresh, N. C. (2005), "The shift team formation problem in multi-shift manufacturing operations", European Journal of Operational Research. Vol. 165. No. 3, pp. 708-728.

Suer, G. A.; Cedeño, A. A. (1996), "A configuration-based clustering algorithm for family formation", Computers & industrial engineering. Vol. 31. No. 1, pp. 147-150.

Tompkins, J.; White, J.; Bozer, Y.; Tanchoco, J. (2003), Facilities planning, Willey, New York.

---

Received: 27 May 2018

Approved: 10 Jun 2018

DOI: 10.14488/BJOPM.2018.v15.n4.a4

How to cite: Delgoshaei, A.; Mirzazadeh, A.; Ali A. (2018), “A Hybrid Ant Colony System and Tabu Search Algorithm for the Production Planning of Dynamic Cellular Manufacturing Systems While Confronting Uncertain Costs”, Brazilian Journal of Operations & Production Management, Vol. 15, No. 4, pp. 499-516, available from: https://bjopm.emnuvens.com.br/bjopm/article/view/501 (access year month day).