A two-phase method for operating room scheduling
José Francisco Ferreira Ribeiro
jffr@fearp.usp.br
São Paulo University – USP, São Paulo, São Paulo, Brazil
Alexandre Bevilacqua Leoneti
ableoneti@usp.br
São Paulo University – USP, São Paulo, São Paulo, Brazil
André Lucirton Costa
alcosta@usp.br
São Paulo University – USP, São Paulo, São Paulo, Brazil
ABSTRACT
In this paper, a two-phase method and a computational program to perform surgery scheduling for operating rooms in a hospital are presented. In Phase I, surgeries are assigned to operating rooms using a generalized assignment model. In Phase II, a sequence for performing surgeries in each room is established. In the proposed method, Phase I maximizes doctors’ room preferences, taking into account the time available in each room, and Phase II establishes a schedule of surgeries in the rooms, according to doctors’ preferences for periods of day. The program was written in Visual Basic for Microsoft Excel and was tested as a surgery scheduling tool at St. Lydia Hospital, Ribeirão Preto, Brazil.
Keywords: Healthcare; Operating Rooms; Scheduling; Sequencing; Optimization.
1 INTRODUCTION
In this paper, a two-phase method and a computational program to help a hospital scheduling team to assign surgeries to be performed in a specific day to the operating rooms available are presented. In Phase I, the mathematical model of generalized assignment is solved to decide which surgeries will be performed in each room. In Phase II, the surgeries’ sequence for each operating room is established.
All surgeries to be scheduled are known in advance, which is a common assumption for elective surgery scheduling problems, in contrast to urgent surgeries. The durations of surgeries are deterministic and cover both surgery times and setup times for the operating rooms (duration = surgery time + setup time).
The model used to assign surgeries to operating rooms is the generalized assignment model (Hillier and Lieberman, 2004). The proposed model maximizes doctors’ room preferences, taking into account the availability of each operating room. Surgery sequencing is performed according to doctors’ preference for performing surgeries at certain periods of the sequence during the day (earlier, intermediate, and later). The results are graphically represented through a Gantt chart.
On Section 2, a literature review on the mathematical models and methods proposed in literature for solving the problem of scheduling operating rooms in ambulatory surgical settings is made. On Section 3, the research methodology is introduced. This two-phase method proposed for operating room scheduling is presented in Session 4. An illustrative example of the proposed method is provided on Section 5. Tests on the proposed method based on data from an 8-month scheduling period of operating rooms were carried out at St. Lydia Hospital, in Ribeirão Preto, Brazil. Results of the computational tests are available on Section 6. On Section 7, it was present a discussion on the proposed method and the results of computational tests. The conclusion is available in Section 8.
St. Lydia Hospital is a city hospital founded in 1960. It was first designed to assist poor children due to the outbreak of polio and meningitis in the Ribeirão Preto area. Presently, it is a general hospital that provides several medical specialties for the population. The surgical center offers surgeries of high, medium and low complexity. To this end, it has four operating rooms and five recovery beds.
The computational program ORP (Operating Rooms Planning) corresponds to the proposed method and was written in Visual Basic for Microsoft Excel. In the program, the generalized assignment model is solved by means of Solver, an add-in for Microsoft Excel, with the preprogrammed branch-and-bound technique (Frontline Solvers, 2016). Solver was chosen due to the efficiency of the branch-and-bound technique (optimal solution), and the popularity and easy access of Microsoft-Excel. Problems with more than 200 decision variables can be solved optimally by OpenSolver for Excel (Mason, 2012), a free Solver version available on the internet (http://opensolver.org/) for bringing solutions for large problems.
The sequencing problem is solved by heuristic procedure in order to obtain an approximate solution, based on (I) doctors’ time preference list and (II) surgery durations. The time available in each operating room is divided in three periods (earlier, intermediate, and later), and the sequencing is performed by a greedy algorithm based on a sorting multi-column procedure (Miles, 2006).
2 LITERATURE REVIEW
Problems of assignment and sequencing are NP-complete (Garey and Johnson, 1977). Due to the algorithmic complexity of the problems, it is not possible to obtain an optimal solution for large examples in reasonable computational time. Therefore, it is often found in literature the proposition of decomposition method and heuristics or approximate algorithms as a solution to the problem.
Jebali et al. (2006) and Aringhieri et al. (2015) decompose the solution of the problem and exploit the inherent hierarchy between the two decision levels. Blake and Donald (2002), Essen et al. (2012), Zhaoxia and Xueping (2014), Dios et al. (2015) Aringhieri et al. (2015) propose a 0/1 programming formulation for assignment and scheduling. Heuristics and metaheuristics are used to solve integer models by Blake and Donald (2002), Dios et al. (2015) and Aringhieri et al. (2015). Marques et al. (2014) propose a genetic algorithm. M’Hallah and Al-Roomi (2014) and Jebali and Diabat (2015) describe a stochastic approach for operating room planning. Zonderland et al. (2010) use queuing theory and Markov decision processes. Donald and Blake (2002), Marques et al. (2014), Zhang et al. (2014) and Dios et al. (2015) describe case studies, respectively, in hospitals of Canada, Portugal, China and Spain. A review of recent operational research methods for operating room planning and scheduling can be found in Cardoen et al. (2010) and Guerriero and Guido (2011).
A review on exact and approximate methods to solve the generalized assignment problem is proposed by Martello and Toth (1992), with different objective functions, transformations, and limits. The large number of methods developed based on branch-and-bound is pointed out in Cattrysse and Van Wassenhove (1992). An extensive and detailed study to compare the performance of heuristics is proposed by Amini and Racer (1994). Öncan (2007) reviews literature on metaheuristics and heuristics. Morales and Romeijn (2005) describe the state of the art. Tabu search metaheuristic is used by Swangnop and Chaovalitwongse (2014) and Mckendall et al. (2015). Quick heuristic algorithms the assignment problem are described by Srivastava and Bullo (2014), Yuan et al. (2014) and Topcuoglu et al. (2014). Lagrangian and dynamic programming are associated in the method proposed by Posta et al. (2012). Woodcock and Wilson (2010) propose branch-and-bound combined with tabu search.
3 METHODOLOGY
This work is an applied research, with the goal of proposing a method and a computational program to help a hospital scheduling team in assigning surgeries to operating rooms. The real data used for the computational tests carried out with the proposed method were provided by Sta. Lydia Hospital, Ribeirão Preto, Brazil.
The proposed method uses a quantitative approach, since decision-making is determined by solving a mathematical model. The model has been solved by Microsoft-Excel-Solver, which was chosen to develop the computational program for the following reasons: (i) Excel is a popular and easy-to-use computer platform, available on most microcomputers, which facilitates access and generates software savings; (ii) the real problems to be solved are small- and medium-sized, within the limit of Microsoft-Excel-Solver decision variables; (iii) Excel Solver has a preprogrammed branch-and-bound technique to solve integer and non-linear problems, able to solve optimally the generalized assignment problem; (iv) because it is a well-known interface, operator training can be facilitated; (v) the decision is presented graphically through the Gantt Chart, facilitating the interpretation of the results and the implementation.
4 METHOD
The proposed method for solving the problem of the daily surgery assignment to operating rooms is composed of two phases: Phase 1: Assignment of Surgeries; Phase II: Sequencing of Surgeries. A computational program corresponding to the proposed method was written in Microsoft-Excel with the aim of automating decision-making.
4.1 Phase I
In the phase assigning surgeries to operating rooms, a generalized assignment problem (Hillier and Lieberman, 2004) is solved. In this problem, there are m surgeries to be performed in n operating rooms, and m > n. The doctor’s preference to perform surgery i in operating room j is equal to pij. Performing surgery i in operating room j requires an amount of time aij of the total time available bj in each room.
Doctor’s preferences for operating rooms (pij) are divided in three levels: higher preference, irrelevant, and undesirable, as shown below:

Let xij be the binary 0/1 variable:

The mathematical model of the generalized assignment problem can be written as follows (1-4):

Subject to:

Objective function (1) maximizes the sum of doctors' preferences for operating rooms. Constraint (2) ensures that each surgery will be performed in a single operating room, and constraint (3) does not allow the total time available in each operating room to be exceeded. Constraint (4) establishes the type of variables as binary.

4.2 Phase II
In the sequencing phase there is a list of surgeries to be performed in each room that was obtained in the previous phase, and the order in which these surgeries will be performed will be set. The time available in each room is divided in three periods: earlier (beginning of the day), intermediate (middle of the day), and later (ending of the day). The doctors’ preference qij for these periods of the sequence is defined below:

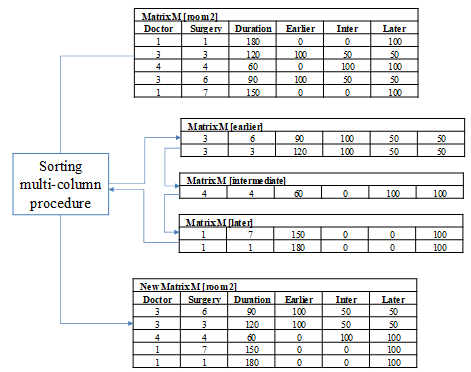
The scheduling is obtained by a greedy algorithm based on the sorting multi-column procedure (Miles, 2006). In contrast to the standard-sort methodology, which sort every data of the matrix using a unique column selected for sorting, the multi-column methodology assumes that each subsequent selected column is the next level of prioritization and thus further defines and refines the sorting. If doctors’ preferences for periods of the sequence are the same, decision is made based on the duration of surgeries: the shortest surgeries are scheduled first.
The pseudocode below summarizes the main steps of the sequencing procedure. Firstly, a matrix M (with the solution obtained in the assignment phase) is sorted in a descending way using the column “earlier” as pivot. Then, surgeries are filtered and stored in a new partial matrix using doctors’ preference qij as criterion. This partial matrix is also sorted using surgeries’ durations, and these surgeries are excluded from M. The same procedure is applied to the column “intermediate” and “later” as a pivot. Finally, all three partial matrixes are jointed in a new sorted matrix M.

5 EXAMPLE
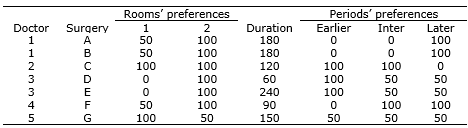
To illustrate the proposed method, the following example is proposed: Five doctors have seven surgeries to be scheduled in two rooms, and there are 10 hours available in each room (600 minutes total). Table 1 presents doctor’s preferences for rooms (aR = 100, bR = 50, cR = 0), doctors’ preferences for periods (aP = 100, bP = 50, cP = 0) and average time for each surgery in minutes (aij).
Table 1. Doctors’ preference for operating rooms
In Phase I, the generalized assignment model given below is solved:
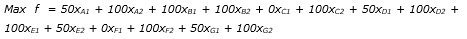
Subject to:
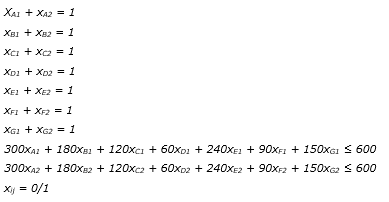
Results obtained on Microsoft Excel add-in Solver are: xA2 = 1, xB1 = 1, xC2 = 1, xD2 = 1, xE1 = 1, xF2 = 1, xG2 = 1 and the other variables are zero. Therefore, surgeries B and E will be assigned to room 1, and surgeries A, C, D, F and G will be assigned to room 2. The sum of preferences of the obtained assignment is equal to (100 + 100) + (100 + 100 + 100 + 100 + 100) = 700, which means the result meets each doctor’s preferences at the maximum level possible.
In Phase II, surgeries are sequenced according to doctors’ preferences for periods of the day. Figure 1 presents the numerical example solved by the sorting multi-column procedure for room 2. The step-by-step procedure for operating room 1 is not presented since only two surgeries have been assigned to this room.
Figure 1. Sequencing procedure with numerical example
Results obtained for rooms 1 and 2 are presented in the Gantt chart shown in Figure 2. Figure 3 shows the main screen (interface) of the computational program (ORP) for two operating rooms.
Figure 2. Gantt chart (room 1 left and room 2 right)
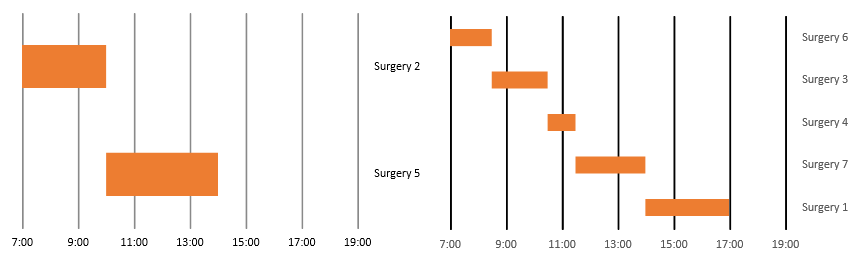
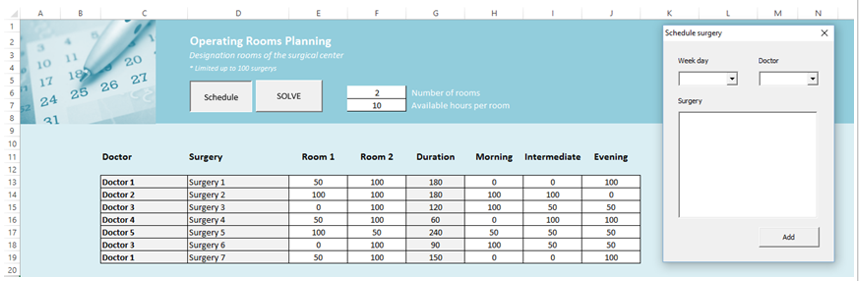
Figure 3. Excel interface for data input of ORP program
6 ST. LYDIA HOSPITAL TEST
St. Lydia Hospital has provided 8-month data in order to create the database and perform computational tests. The number of surgeries performed by month is 216, 180, 78, 135, 172, 301, 308 and 238, respectively from January to August 2017.
The test shown below was performed on July 3rd, 2017 (with the largest number of surgeries): We aimed to assign and schedule 21 surgeries to four operating rooms available. The model to solve the assignment problem has 21×4 = 84 binary 0/1 variables. In order to preserve data confidentiality, we do not mention types of surgeries or doctors’ names in the paper.
6.1 Data
Table 2 shows St. Lydia Hospital database on July 3rd: 21 surgeries, 8 doctors, surgery’ durations, and doctors’ preferences for operating rooms and for periods of the day.
Table 2. Santa Lydia database, July 3rd, 2017
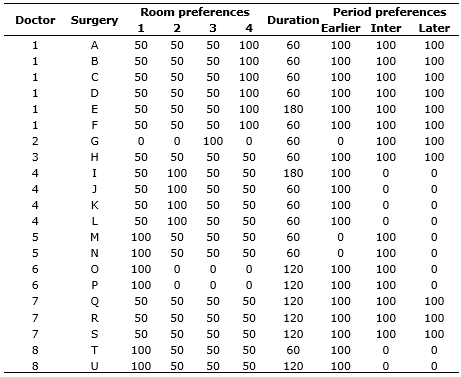
The St. Lydia Hospital Scheduling Team reported that: 1) Doctors’ preferences for rooms are mainly related to operational aspects and the surgical equipment’ position in the operating rooms. Then, doctors have to inform their preferences; 2) Surgery duration may be significantly longer or shorter, according to the doctor performing it. Then, surgery duration is provided individually for each doctor; 3) Doctors’ preferences for periods may be different for each day of the week. Then, doctor’ preferences for periods are provided separately.
There is a window in the program ORP to enter all data related to doctors, surgeries, and preferences for rooms and for times of day, which are stored on spreadsheets “Doctors”, “Surgeries”, “Preferences for Rooms” and “Preferences for Periods of the Day”, respectively. The program displays results in a Gantt chart. If the problem is infeasible a message is presented warning the user.
The program ORP always takes less than five seconds to find results on all tests performed on St. Lydia Hospital database, on a computer with an Intel Core 2 Duo processor and 4GB of RAM.
6.2 Assignment
Results obtained on Microsoft Excel add-in Solver were: xH1 = 1, xM1 = 1, xN1 = 1, xO1 = 1, xP1 = 1, xT1 = 1, xU1 = 1, xI2 = 1, xJ2 = 1, xK2 = 1, xL2 = 1, xR2 = 1, xS2 = 1, xG3 = 1, xA4 = 1, xB4 = 1, xC4 = 1, xD4 = 1, xE4 = 1, xF4 = 1, and xQ4 = 1 and the other variables are zero. Therefore, surgeries H, M, N, O, P, T and U will be assigned to room 1; surgeries I, J, K, L, R and S will be assigned to room 2; surgery G will be assigned to room 3; and surgeries A, B, C, D, E, F and Q will be assigned to room 4. The sum of preferences of the assignment obtained is equal to 1900, which means the result meets each doctor’s preferences as much as possible. The time available in each room was 600 minutes (10 hours), and there was only one room that presented idle time. Rooms 1, 2, 3 and 4 were assigned 600, 600, 60 and 600 minutes, respectively.
6.3 Sequencing
Sequencing is performed based on doctors’ preferences for three periods of the day: earlier, intermediate, and later. In case of conflict between doctors’ preferences, surgeries are sequenced according to their duration: Shorter surgeries are performed first. This decision criterion was established by the St. Lydia Hospital Scheduling Team.
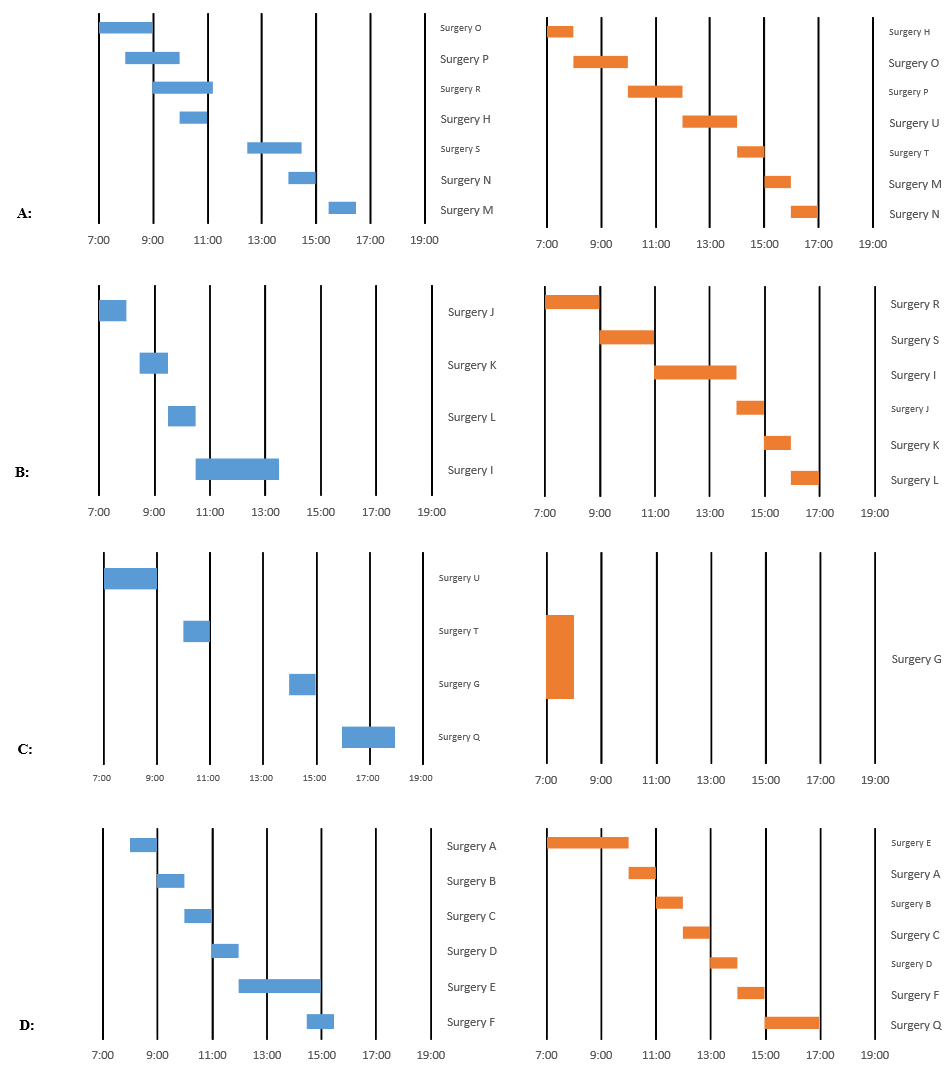
Figures 4 (A–D) show Gantt charts corresponding to the solution obtained by ORP program (ORP solution). These results can be compared with the results obtained manually by the St. Lydia Hospital Scheduling Team (current solution).
The scheduling proposed by the ORP program was considered very appropriate by the St. Lydia Hospital Scheduling Team: data were easily entered into the program, results were obtained quickly, and all constraints and preferences were met.
Figure 4. Results comparing current solution (left) and ORP solution (right)
7 DISCUSSION
In some tests we had to arbitrate doctor’s preferences for operating rooms and doctor’s preferences for periods of the day, because some doctors indicated no particular interest in classifying operating rooms. Thus, the objective function became irrelevant, and the result was considered only feasible. In other tests, we decided to conduct new interviews with doctors and readjust preference values.
In general, results obtained by the ORP program were considered satisfactory for the St. Lydia Hospital Scheduling Team, since the computational program always used the same number of operating rooms or even one or two operating rooms less than the solution obtained manually by the St. Lydia Hospital Scheduling Team in all tests performed.
Different from other contributions in the literature, Excel was used to develop the program because it is very popular and widespread software. The association between VBA language and Excel allowed presenting results in an intuitive way by Gantt chart, making the computational program very easy to use and decision making simpler.
Results obtained in computational tests performed always demanded less than five seconds. The assignment phase takes more computational time than the sequencing phase: In general, for each minute required in the assignment phase (solved by branch-and-bound technique), the sequencing phase requires only one second (solved by greedy algorithm).
8 CONCLUSION
In this paper we presented a two-phase method and a program to perform surgery scheduling for operating rooms in a hospital. The method consists of the following phases: (I) Assignment and (II) Sequencing. In the Assignment phase a mathematical model in binary variables 0/1 based on the generalized assignment model was proposed to assign surgeries to operating rooms in a hospital. The model was solved by branch-and-bound technique in order to obtain the optimal solution for the problem and thus ensure the best possible use of the operating rooms.
In the Sequencing phase surgeries are scheduled in the rooms according to doctors’ preferences for time of day: earlier, intermediate, and later. The procedure is greedy, using sorting prioritization. The result of the sequencing phase is presented on a Gantt chart, in which each bar is associated with one operating room. The duration of the surgery in operating rooms is given by its length in the bar on the Gantt chart.
The main contributions of this research are: (i) proposition of an original model for solving the assignment problem based on the classical model of generalized assignment; (ii) decomposition of the problem resolution in two phases: assignment and sequencing, which allows solving sub problems of reduced size in a very reasonable time; (iii) development of an Excel program, one of the most popular software in the history of computing.
The proposed method for surgery scheduling in operating rooms was tested at St. Lydia Hospital, Brazil. The hospital has provided us with data from an 8-month scheduling period for the operating rooms. The results obtained with the aid of the program have decreased, in average, by one (even 2 in 4) the number of rooms used. The St. Lydia Hospital Scheduling Team has considered the program very simple to use, and the results very good and encouraging.
The program corresponding to the two-phase method proposed was written in VBA language (Visual Basic) for Microsoft Excel. All tests performed gave results in less than five seconds. Microsoft-Excel was chosen for the development of this work with the objective of providing simplicity to the program, and greater accessibility and popularity among users, technicians, and decision makers.
REFERENCES
Amini, M. M.; Racer, M. (1994). A rigorous computational comparison of alternative solution methods for the generalized assignment problem, Management Science, Vol. 40, No. 7, pp. 868-890, available from: https://doi.org/10.1287/mnsc.40.7.868 (access 16 Oct 2018).
Aringhieri, R.; Landa, P.; Soriano, P.; Tanfani, E.; Testi, A. (2015). A two level metaheuristic for the operating room scheduling and assignment problem, Computers & Operations Research, Vol. 54, pp. 21-34, available from: https://doi.org/10.1016/j.cor.2014.08.014 (access 16 Oct 2018).
Blake, J. T.; Donald, J. (2002). Mount Sinai Hospital uses integer programming to allocate operating room time, Interfaces, Vol. 32, No. 2, pp. 63-73, available from: http://strategygen.com/wp-content/uploads/9fcfd510fb79c8645d.pdf (access 16 Oct 2018).
Cattrysse, D. G.; Van Wassenhove, L. N. (1992). A survey of algorithms for the generalized assignment problem, European Journal of Operational Research, Vol. 60, No. 3, pp. 260-272, available from: https://doi.org/10.1016/0377-2217(92)90077-M (access 16 Oct 2018).
Cardoen, B.; Demeulemeester, E.; Belien, J. (2010). Operating room planning and scheduling: A literature review, European Journal of Operational Research, Vol. 201, No. 3, pp. 921-932, available from: https://doi.org/10.1016/j.ejor.2009.04.011 (access 16 Oct 2018).
Dios, M.; Molina-Pariente, J. M.; Fernandez-Viagas, V.; Andrade-Pineda, J. L.; Framinan, J. M. (2015). A Decision Support System for Operating Room scheduling, Computers & Industrial Engineering, vol. 88, pp. 430–443, available from: https://doi.org/10.1016/j.cie.2015.08.001 (access 16 Oct 2018).
Essen, J. T.; Hurink, J. L.; Hartholt, W.; Akker, B. J. (2012). Decision support system for the operating room rescheduling problem, Health Care Management Science, Vol. 15, No. 4, pp. 355-372, available from: https://doi.org/10.1007/s10729-012-9202-2 (access 16 Oct 2018).
Frontline Solvers (2016), available from: http://www.solver.com/excel-solver-integer-programming (access 1 Dec 2017).
Garey, M. R.; Johnson, D. S. (1977). Computers and intractability: a guide to the theory of NP-completeness, Freeman.
Guerriero, F.; Guido, R. (2011). Operational research in the management of the operating theatre: a survey, Health Care Management Science, Vol. 14, No. 1, pp. 89-114, available from: https://doi.org/10.1007/s10729-010-9143-6 (access 16 Oct 2018).
Hillier, F. S.; Lieberman, G. J. (2004). Introduction to Operations Research, McGraw-Hill.
Jebali, A.; Alouane, A. B. H.; Ladet, P. (2006). Operating rooms scheduling, International Journal of Production Economics, Vol. 99, No. 1-2, pp. 52–62, available from: https://doi.org/10.1016/j.ijpe.2004.12.006 (access 16 Oct 2018).
Jebali, A.; Diabat, A. (2015). A stochastic model for operating room planning under capacity constraints, International Journal of Production Research , Vol. 53, No. 24, pp. 7252-7270, available from: https://doi.org/10.1080/00207543.2015.1033500 (access 16 Oct 2018).
Mckendall, A.; Iskander, W.; Mckendall, S.; Chester, A. (2015). An application of a generalised assignment problem: Assigning recruiters to geographical locations, International Journal of Operational Research, Vol. 22, No. 1, pp. 31-47, available from: https://doi.org/10.1504/IJOR.2015.065938 (access 16 Oct 2018).
Martello S.; Toth P. (1992) Generalized assignment problems. In: Ibaraki T., Inagaki Y., Iwama K., Nishizeki T., Yamashita M. (eds) Algorithms and Computation. ISAAC 1992. Lecture Notes in Computer Science, Vol 650. Springer, Berlin, Heidelberg, available from: https://doi.org/10.1007/3-540-56279-6_88 (access 16 Oct 2018).
Marques, I.; Captivo, M. E.; Pato, M. V. (2014). Scheduling elective surgeries in a Portuguese hospital using a genetic heuristic, Operations Research for Health Care, Vol. 3, No. 2, pp. 59-72, available from: https://doi.org/10.1016/j.orhc.2013.12.001 (access 16 Oct 2018).
Mason, A. J. (2012). OpenSolver – An open source add-in to solve linear and integer programmes in Excel, Operations Research Proceedings 2011, pp. 401-406, available from: http://dx.doi.org/10.1007/978-3-642-29210-1_64 (access 16 Oct 2018).
M’Hallah, R.; Al-Roomi, A. H. (2014). The planning and scheduling of operating rooms: A simulation approach, Computers & Industrial Engineering, Vol. 78, pp. 235-248, available from: https://doi.org/10.1016/j.cie.2014.07.022 (access 16 Oct 2018).
Miles, D. B. (2006). A user-centric tabular multi-column sorting interface for intact transposition of columnar data, PhD Thesis BYU, Utah, USA, available from: https://scholarsarchive.byu.edu/cgi/viewcontent.cgi?article=1343&context=etd (access 1 Dec 2017).
Morales, D. R.; Romeijn, H. E. (2005). The generalized assignment problem and extensions. in D-Z Du & PM Pardalos (eds), Handbook of Combinatorial Optimization: Supplement Volume B., Springer, Boston, MA, pp. 259-311, available from: https://doi.org/10.1007/b102533 (access 1 Dec 2017).
Öncan, T. (2007). A survey of the generalized assignment problem and its applications, INFOR: Information Systems and Operational Research, Vol. 45, No. 3, pp. 123-141, available from: https://doi.org/10.3138/infor.45.3.123 (access 16 Oct 2018).
Posta, M.; Ferland, J. A.; Michelon, P. (2012). An exact method with variable fixing for solving the generalized assignment problem, Computational Optimization and Applications, Vol. 52, No. 3, pp. 629-644, available from: https://doi.org/10.1007/s10589-011-9432-0 (access 16 Oct 2018).
Srivastava, V.; Bullo, F. (2014). Knapsack problems with sigmoid utilities: Approximation algorithms via hybrid optimization, European Journal of Operational Research, Vol. 36, No. 2, pp. 488-498, available from: https://doi.org/10.1016/j.ejor.2013.12.035 (access 16 Oct 2018).
Swangnop, S.; Chaovalitwongse, P. (2014). A two-step tabu search heuristic for multi-period multi-site assignment problem with joint requirement of multiple resource types, Engineering Journal, Vol. 18, No. 3, pp. 83-97, available from: https://doi.org/10.4186/ej.2014.18.3.83 (access 16 Oct 2018).
Topcuoglu, H. R.; Ucar, A.; Altin, L. (2014). A hyper-heuristic based framework for dynamic optimization problems, Applied Soft Computing, 19, pp. 236-251, available from: https://doi.org/10.1016/j.asoc.2014.01.037 (access 16 Oct 2018).
Woodcock, A. J.; Wilson, J. M. (2010). A hybrid tabu search / branch & bound approach to solving the generalized assignment problem, European Journal of Operational Research, Vol. 207, No. 2, pp. 566-578, available from: https://doi.org/10.1016/j.ejor.2010.05.007 (access 16 Oct 2018).
Yuan, M.; Jiang, C.; Li, S.; Shen, W.; Pavlidis, Y., Li J. (2014). Message passing algorithm for the generalized assignment problem. In: Hsu CH.; Shi X.; Salapura V. (eds), Network and Parallel Computing. NPC 2014. Lecture Notes in Computer Science, Vol. 8707. Springer, Berlin, Heidelberg, available from: https://doi.org/10.1007/978-3-662-44917-2_35 (access 16 Oct 2018).
Zhaoxia, Z.; Xueping, L. (2014). Scheduling elective surgeries with sequence-dependent setup times to multiple operating rooms using constraint programming, Operations Research for Health Care, Vol. 3, No. 3, 2014, pp. 160-167, available from: https://doi.org/10.1016/j.orhc.2014.05.003 (access 16 Oct 2018).
Zonderland, M. E.; Boucherie, R. J.; Litvak, N.; Vleggeert-Lankamp, C. L. A. M. (2010). Planning and scheduling of semi-urgent surgeries, Health Care Management Science, Vol. 13, No. 3, pp. 256-267, available from: https://doi.org/10.1007/s10729-010-9127-6 (access 16 Oct 2018).
Received: 18 Dec 2017
Approved: 16 Oct 2018
DOI: 10.14488/BJOPM.2018.v15.n4.a1
How to cite: Ribeiro, J. F. F.; Leoneti, A. B.; Costa, A. L. (2018), “A two-phase method for operating room scheduling”, Brazilian Journal of Operations & Production Management, Vol. 15, No. 4, pp. 471-480, available from: https://bjopm.emnuvens.com.br/bjopm/article/view/421 (access year month day).