Advertisement quantity optimization to maximize profit in a Publishing House
Natalia Boff Medeiros
nbmedeiros@ucs.br
University of Caxias do Sul – UCS, Caxias do Sul, Rio Grande do Sul, Brazil.
Gabriel Vidor
gvidor@ucs.br
University of Caxias do Sul – UCS, Caxias do Sul, Rio Grande do Sul, Brazil.
Abstract
This study aims to determine the optimal quantity of pages and the optimal quantity of each size advertisement that a magazine should have to maximize profit in a publishing house. The solution of this problem is based on operations research method application and is composed by four steps: (i) defining the problem, (ii) algorithm application, (iii) modeling scenarios and (iv) decision-making. The application of the method is performed in a publishing house data and the problem is solved by linear programming perspective. The results indicate that it is possible to maximize the total profit finding the optimal quantity of advertisements. The main contribution of the paper is to illustrate the use of operations research at service industries through a publishing house case. In conclusion, the method proposed to improve the ads allocation regarding the maximum profit.
Keywords: optimization; operations research; publishing house; advertisements.
1 Introduction
The need to make the best decisions about the use of the available resources in World War II emerged from the use of optimization problems (Dym, 2004). Optimization is the process to make something perfected, in other words, make your performance the most efficient possible (Christensen et Bastien, 2015). Furthermore, optimization is an important concept that leads to the idea of achieving the best result or finding the optimal outcome, maximizing the gain, profit, output, performance or efficiency (Dym, 2004; Yang, 2013). The importance of the optimization is based on the uncertainty and on the limitation of resources, such as time, space and money, and for these reasons, it has a vast range of applications (Yang, 2013). The search for optimal results for a problem is based in a good decision making, once, in most real-world cases, the parameters and factors that affect the problem are very complicated and, for this reason, to make a decision is a challenge (Dym, 2004; Yang, 2013). To support the decision-making, an optimization problem needs to be modeled through an objective determination, which is the structure that will be optimized, and the variables that are the parameters that will be changed in the optimization process (Christensen et Bastien, 2015). An optimization problem depends on the formulation of an objective function, whose extreme values will be returned, as well as the constrains that limit the variables values to guide toward a small number of solutions (Christensen et Bastien, 2015; DYM, 2004). The decision-making is based on the modeling of the optimization problems, solving the problem through software and analyzing the results obtained (Zakharova et Minashina, 2015).
The science that studies the optimization problems is called Operations Research (OR). After the World War II, the OR was introduced to the industry area to improve the productivity, obtaining a fast diffusion and great results (Xing et al., 2013). Supported by the growth of the service industry role in the modern economy, OR began to be applied in the context of the service sector. Although the service system is more complex than the manufacturing system, once the service industry produces intangible services while the manufacturing industry produces tangible products, the number of OR studies focused on the service system is increasing (Xing et al., 2013). The analysis framework from the article “Operations Research (OR) in Service Industries was: A Comprehensive Review” analyzed the applications in service industries articles published in 17 OR journals from 2007 to 2013. The analysis showed that about 5% of the articles from the journals are applications in service industries.
The service industry has a lot of branches, including the publicity branch that aims to offer to a client, usually entrepreneurs, service providers and industries, an opportunity to increase your visibility and attract more customers and users. The publicity industry faces many challenges every day, and the operations research could be applied to help the companies to maximize their profit. One problem that is always present in the advertisement management is the capability to allocate the maximum number of ads aiming the maximum revenue. A literature review about the application of optimization in the publicity industry showed that there is a little number of articles available.
Marszałkowski et Drozdowski (2013), propose a method to optimize the column widths from a website layout for a given set of advertisement units; each ad unit with its width and height measured in pixels. The layout partitioning, which is the action of dividing the website into columns, needs to consider the aesthetically pleasing and is made in an arbitrarily way. For this reason the layout partitioning is treated as a combinatorial optimization problem, once the ad units do not have a unification or standardization and can be compared to a factory layout optimization. The method uses Wang two-dimensional constrained cutting stock algorithm to join the ad units that fit the given column widths and find the feasible combinations, evaluating the column widths for several objective functions and finding the best solution from the list of layouts founded. The results that each dataset, with different page width results in different sets of layout show that the input parameters need to be correctly configured for each website.
Boskamp et al. (2011), proposes the use of heuristics algorithms to solve the Web banner advertisements allocation problem. This problem is classified as two-dimensional, single, orthogonal, and knapsack. The objective of the author is to maximize the revenue, finding a suitable pattern, generating algorithm. A brute force search algorithm was implemented and resulted in a huge time-consuming to find the optimal solution. In contraposition, four heuristic algorithms are tested: the left justified algorithm, the orthogonal algorithm, the GRASP constructive algorithm, and the greedy stripping algorithm, configuring each simulation with one of the three different parameters that include the size of the banner, the sorting of the advertisements and the algorithm. The analyses of the algorithms showed that they differ in their effectiveness and efficiency. The most effective algorithm was the orthogonal and the most efficient was the greedy stripping.
Kumar et al. (2006), also propose the heuristics algorithms to solve the schedule advertisements on the web problem in order to maximize revenue. However, besides the analyses of the advertisement size, other two factors are considered: the time amount that the ad appears and the number of possible visualizations of the ad. The authors developed the Largest Size Most Full (LSMF) heuristic and used a Genetic Algorithm (GA) to solve the problem. Then, they combined the GA with LSMF and an existing algorithm, and developed a hybrid GA. When comparing the existing approach with the developed one, the performance of the hybrid GA is better than the GA algorithm, proving that the use of the developed algorithm can improve the revenue of the web advertisement schedule.
In these scenarios, a publishing house that produces magazines with advertisements wants to maximize the total profit per magazine produced. The advertisement allocation has a great influence in the publishing house revenue, and is made after selling the ads, fitting randomly one by one. This fitting way leads to a poor space use. The publishing house has a salesman that sells advertisements for companies and stores that wants more visibility in order to attract new clients. The companies and stores can buy five different sizes of advertisements, each with a different price, and they compose the total revenue. The publishing house has limitations in terms of the number of pages per magazines and also has a cost that composes the total cost along with the salary of the salesman. Therefore, in order to maximize the profit, what should be the optimal quantity of pages that the magazine should have, and also, what should be the quantity of each ad size that the salesman should sell?
To improve the profit of the publishing house and solve the problem about the optimal quantities, a linear programming can be created including the variables that need to be decided and also the restrictions about the problem.
2 Research Methodology
The research methodology of this article is based on four steps: (i) defining the problem, (ii) algorithm application, (iii) modelling scenarios and (iv) decision-making. The four steps are explained above.
2.1 Defining the problem and model description
First of all, it is important to define the problem that will be solved with the algorithm application. To a good definition, it is necessary to have accurate information in terms of all the processes and parameters that affect the problem. It is important to observe the deportment of the data and the characteristics of the situation. To describe the model, the first step is to define the variables of the problem, that is, the parameters that will be changed (Christensen et Bastien, 2015) and that will affect the revenue. Afterwards, it is necessary to define an objective function that is the definition of the optimization problem, once this is the function that will achieve a maximum or a minimum value (Zakharova et al., 2015). Equation 1 demonstrates the objective function that leads to a maximum or minimum value, where x1, x2,…, xm are the variables.
f(x1,x2,…,xm) → (max,min) (1)
With the variables and the objective function defined, it is necessary to extract from the data the information that limits the variables’ values (Christensen et Bastien, 2015; Dym, 2004). Equation 2 demonstrates a constraint where x1,x2,…,xm are the variables and the bi is the maximum value that the function can assume.
g(x1,x2,…,xm) ≤ bi (2)
2.2 Algorithm application
After the problem is defined, it is possible to solve the problem through an algorithm. The algorithm used depends of the model type described.
2.3 Modelling scenarios
The model can be modified to observe scenarios where the constraints can be different from the current reality. These scenarios can show to the company the modifications that will result or not in a profit increase.
2.4 Decision-making
The decision-making is the final step of the methodology and is based on the other steps. With the results of the algorithm application and the scenarios simulated, it is possible to analyze the optimal solution and also, the possible modifications in the problem. It is important to have a critical thinking to make the best decision for the company, using the results to structure the processes.
3 Case description
A publishing house produces magazines for many cities in the south of Brazil. The magazines are focused on manufacturing workers and their families. The company is composed by one salesman, one graphic designer and one administrator. The salesman receives a salary that varies according to the quantity of advertisements sold. Usually, the magazines are produced once every three months due to the time needed to sell the advertisement; the time for the graphic designer to create the advertisement; and the time for printing the magazines. The profit of the publishing house is the revenue, which is composed by the selling price of the advertisement, minus the total cost, which is composed by the salesman salary and by the printing costs.
The magazine is composed by advertisements that are bought by factories, companies, stores and service providers, such as doctors, dentists, mechanics and hairdressers, aimed to show the manufacturing workers the services provided by their city. Also, to organize the magazine and to facilitate the handling by the readers, the magazine has a table of contents that lists advertisers and indicates in which page the advertisement is located. The table of contents increases with the number of advertisements and it is estimated that each advertisement needs a space of 2 % of one page. Customers can choose five types of advertisements; each one has different sizes and different prices. The sizes are represented in figure 1.
Figure 1. Sizes representation
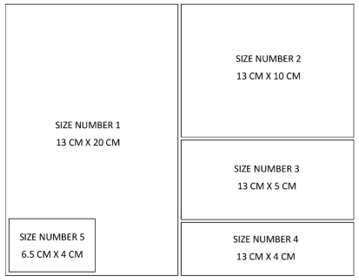
Source: The author(s)’ own.
The advertisement of size number 1 has a width of thirteen centimeters and a height of twenty centimeters; thus, the size number 1 fits exactly in one page. The advertisement of size number 2 has 13 centimeters width and ten centimeters of height; thus, two size-2 advertisements can be placed in one page. Size-3 advertisement has thirteen centimeters of width and five centimeters of height; thus, one page fits four advertisements of size number 3. Size-4 advertisement has thirteen centimeters of width and four centimeters of height; in this way, five advertisements of size number 4 could be placed in one page of the magazine. Lastly, the advertisement of size number 5 is the smallest and has six and a half centimeters of width and four centimeters of height. Ten advertisements of size number 5 can be placed in one page
The bigger the advertisement is, the more visibility the client will have; however, it will be more expensive. For this reason, the advertisement selling prices increase according to its size. The selling prices are: R$ 375.00 for an advertisement size number 1; R$ 225.00 for an advertisement size number 2; R$ 185.00 for an advertisement size number 3; R$ 150.00 for an advertisement size number 4 and R$ 125.00 for an advertisement size number 5.
The pages of the magazine can contain just one size of advertisement or there can be a combination of some sizes. The only rule is that the advertisements need to fit in one page; in other words, the sum of the height of the advertisements placed in one page cannot exceed the height of twenty centimeters. Moreover, the pages cannot have a blank space. For this reason, the number of advertisements size number 5 needs to be multiple of two, once this size is the only one that is half wide in relation to the other sizes. If the number of advertisements size number 5 is an odd number, then the magazine will have a blank space once any other size can fit in this space.
The salesman of the publishing house receives a salary that varies according to the quantity of advertisements sold. The salary is composed by a fixed cost for opening the market for one size, in other words, a fixed cost for selling one type of size and also a cost per advertisement sold. The fixed costs for each size are R$ 300.00 for advertisements size number 1; R$ 250.00 for advertisements size number 2; R$ 150.00 for advertisements size number 3; R$ 100.00 for advertisements size number 4; and R$ 50.00 for advertisements size number 5. In this way, for example, if the salesman sells one advertisement or more of size number 3, then the salary of the salesman will have the fixed cost for selling this size of R$ 150.00. In addition, the cost per advertisement decrease according to the decrease of the size, since the smaller the advertisement is, the easier it is to sell. The smaller advertisement sizes generate a low selling cost, while the bigger ones generate a high selling cost. The costs per advertisements are R$ 100.00 per advertisement size number 1; R$ 50.00 per advertisement size number 2; R$ 30.00 per advertisement size number 3; R$ 20.00 per advertisement size number 4; and R$ 10.00 per advertisement size number 5.
The publishing house has contracts with some big companies that always buy advertisements of the biggest size, and they request, at least, 5% of the advertisements of the biggest type. On the other hand, the publishing house is aware that small companies that want to advertize in the magazine cannot afford the biggest size; thus, they usually buy the smallest size. In order to give opportunity to small companies, the magazine should spare, at least, 10 % of its smallest size advertisement for them.
The magazines are usually done in small cities; thus, it is usually difficult to find more than 300 customers that want to buy advertisement in just one city. For this reason, the publishing house created a limit in the number of advertisements. This limit should not exceed 300 advertisers.
The last part of producing a magazine is printing it and distributing it to the manufacturing workers in the city. The publishing house estimates an average number of manufacturing workers in cities and uses this average to print a fixed number of copies for all cities. Thus, the publishing house always prints three thousand issues and the cost for printing them is always calculated per issue. The printing cost of the magazine is calculated according to the number of pages. The cost is composed by two parts: the first part is the cost per page and the second one is a fixed maintenance cost. The maintenance is done more than once and the regularity varies according to the range that the number of pages is included. Thus, with the increase in the number of pages, the frequency of the maintenance of the magazine also increases. Therefore, the fixed maintenance cost increases with the number of pages. Thus, if the number of pages is between 1 and 20 pages, the fixed cost of maintenance is R$ 500.00. The fixed cost of maintenance for a number of pages between 21 and 40 pages is R$ 1,000.00. The fixed maintenance cost is R$ 1,500.00 if the number of pages is between 41 and 60 pages. And finally, if the number of pages is between 61 and 80 pages, the fixed maintenance cost is R$ 2,000.00.
One restriction for printing the magazine is that the printer prints four pages at a time, since four pages can be fitted in an A4 sheet. Thus, the magazine needs to have a number of pages that is multiple of four to avoid blank pages. In addition, the printer cannot group more than 80 pages with good quality for the reader. Therefore, the limit of pages that the printer can print is 80.
4 Methodology Applicability
4.1 Defining the problem and model description
The problem of the case is based on how many pages the magazine should have and which quantity of each size of advertisements should the publishing house sell to maximize profit. The model description is showed below.
4.1.1 Variables
The model needs variables that will represent the numbers that need to be decided. First, the model should have a set of variables that will represent the quantity of advertisements of each size that need to be sold in order to have the maximum profit.
X1 - Number of advertisements size number 1 that should be sold.
X2 - Number of advertisements size number 2 that should be sold.
X3 - Number of advertisements size number 3 that should be sold.
X4 - Number of advertisements size number 4 that should be sold.
X5 - Number of advertisements size number 5 that should be sold.
In addition, the model needs a variable that indicates the number of pages (P_g_) and a variable that indicates the size of the table of contents (T_c_), because this size varies according to the number of advertisements sold. Also, the model should contain a variable for the printing fixed cost (F_c_) that varies according with the range that the number of pages is included.
To help the constraint that requests that the number of advertisements of size number 5 should be multiple of two and the constraint that explains that the number of pages needs to be a multiple of four, two integer variables are needed, Int2 and Int4.
The sales representative earns fixed values for selling one size of advertisement or not; Thus, to decide whether one size should be sold or not, the model needs binary decision variables.
Y1 - 1 if the salesman should sell advertisements of size 1; 0 if not
Y2 - 1 if the salesman should sell advertisements of size 2; 0 if not
Y3 - 1 if the salesman should sell advertisements of size 3; 0 if not
Y4 - 1 if the salesman should sell advertisements of size 4; 0 if not
Y5 - 1 if the salesman should sell advertisements of size 5; 0 if not
In a similar way, to determine in what range the number of pages is included, the model needs binary decision variables that will describe whether the number of pages is included in a determined range or not.
W1 - 0 if the number of pages is in the range 1; 1 if not
W2 - 0 if the number of pages is in the range 2; 1 if not
W3 - 0 if the number of pages is in the range 3; 1 if not
W4 - 0 if the number of pages is in the range 4; 1 if not
4.1.2 Objective function
The objective function is composed by the total revenue and the total cost and represents the total profit of the publishing house. The total revenue is composed by the sum of the selling price of each advertisement size times the quantity that should be sold. The total cost is composed by the salary of the salesman and the printing cost. The salary of the salesman has the cost per advertisement sold times the quantity of each advertisement size and for the fixed cost for opening the market for one size times the decision variable that confirms whether the salesman should sell one type of advertisement or not. The printing cost includes the fixed printing cost that varies according to the range that the number of pages is included and also for the cost per page.
Max Z = R – C (3)
where
R = 375X1+225X2+185X3+150X4+125X5 (4)
C = 100X1+50X2+30X3+20X4+10X5 + 300Y1+250Y2+150Y3+100Y4+50Y5+Fc+50Pg (5)
4.1.3 Constraints
The model needs constraints that will represent all the restrictions that the publishing house has to allocate the advertisements and to produce the magazine. These constraints contain all the information that can modify the result of the problem.
The major constraint is about the space of the magazine. The sum of the space occupied by all advertisements and the space occupied by the table of contents should be equal to the number of pages. The space occupied by one advertisement of size number 1 is 100 % of one page; thus, the weight of the variable that represents the quantity of advertisements that should be sold of this size is 1. One advertisement size number 2 represents 50 % of one page, one advertisement size number 3 represents 25 % of one page, one advertisement size number 4 represents 20 % of one page and one advertisement size number 5 represents 10 % of one page. Accordingly, the variable that represents the quantity of advertisements that should be sold of these sizes should have a weight of 0.5, 0.25, 0.2 and 0.1, respectively.
The maximum number of pages is limited to 80, which leads to a constraint that determines that the pages variable needs to be less than or equal to 80. Also, the number of pages needs to be a multiple of 4; thus, the page variable divided by 4 needs to be an integer number.
The size of the table of contents increase in 2 % of one page with each advertisement sold. For this reason the table of contents variable needs to be equal to 2% of the ads quantity sums. In order to limit the number of advertisements, the total quantity of them needs to be less than or equal to 300.
The number of advertisements number 1 should be at least 5% of the sum of the advertisements due to the contracts with big companies, thus the number 1 quantity variable X1 should be greater than or equal to 5% of the total quantity of advertisements. Similarly, the number 5 quantity variable X5 should be greater than or equal to the ads quantity sum once the number of advertisements of number 5 should be at least 10 % of the sum of the advertisements in order to give opportunity to the small companies. The X5 variable also needs to be multiple of 2 because there is no other size that fits the page with it, as this size has a width that is half the other sizes.
Thus, the number 5 quantity divided by 2 should be an integer number.
To know what types of advertisements should be sold to include the salesman fixed salary for each one, the constraint should set the Yi to 1 or 0. Furthermore, if the salesman should sell one type of advertisement, then the Xi should be less than or equal to the maximum number of advertisements that fit in 80 pages, which is the maximum limit of pages.
The fixed printing cost is adjusted according to the range that the number of pages is included. The constraint should be an if-then one where the number of pages variable is tested according to the range and then, the fixed printing cost variable is determined. To test the number of pages variable, it is necessary to use binary variables that will assume the value 1 if the test is positive and 0 if the test is negative. The last constraint indicates that the sum of these variables should be equal to the range quantity minus one.
4.1.4 General algebraic representation
Indices
Number of size index i = 1, 2, 3, 4, and 5 corresponding to size number 1, size number 2, size number 3, size number 4 and size number 5.
Range index j = 1, 2, 3 and 4 corresponding to range 1, range 2, range 3 and range 4.
Multiple integer index k = 2 and 4 corresponding to the multiple of 2 and the multiple of 4.
Parameters
Spi = selling price for advertisement of size number i
Cpai = cost per advertisement of size number i for the salary of the salesman
Sfci = salesman salary fixed cost for selling advertisements of size number i
Swi = space weight for advertisement of size number i
Li = limit of advertisements of size number i that fits in 80 pages
Fj = fixed cost of maintenance for the range j
Ubj = upper bound of range j
M = is a large number
Variables
Xi = number of advertisements of size number i that should be sold.
Yi = 1 if the salesman should sell advertisements of size number I; 0 if not.
Wj = 0 if the number of page is in the range j; 1 if not.
Pg = number of pages that the magazine should have
Tc = size of the table of contents
Fc = fixed printing cost
Intk = integer variable that indicates if the result is multiple of k.

4.2 Algorithm Application
To solve the problem it was necessary to put the data on the Excel and utilize the Solver to find an optimal solution. A table of variables was created with each variable that the model has. Moreover, a table of costs was created to help in the constraints.
A cell that contains all the total revenue and the total cost is the objective function. The constraints were created with the left hand side with the formulas and the right hand side with the limits. After all the variables were created and the objective function and the constraints were settled, the optimal solution was found through the Solver.
The software application led to an optimal result. The optimal quantity of page is 80, and the optimal advertisements quantities that the salesman should sell are 15 advertisements of size number 1, 200 advertisements of size number 3, five advertisements of size number 1 and 80 advertisements of size number 5. The table of contents occupies six pages. The total revenue is R$ 53,375.00 and the total cost is R$ 15,000.00, totalizing a max profit of R$ 38,375.00.
The magazine will have 15 pages with one advertisement size number 1 per page, 50 pages with four advertisements size number 3 per page, 1 page with five advertisements size number 4 and eight pages with ten advertisements size number 5 per page, as shown in figure 2.
Figure 2. Representation of the optimal result

Source: The author(s)’ own.
4.3 Modeling scenarios
The optimal result shows the optimal quantities according to the current reality; however, the model can be modified in order to observe whether different constraints can result in a profit increase. A sensitivity analysis can be done in the limit of pages. Increasing the number of pages changes the total profit only in numbers multiple of four. The total profit has a small increase and the profit per page has a decrease. Therefore, it is not profitable to increase the number of pages once the profit increases less than R$ 1,000.00 per each additional four pages and the profit per page decreases more than R$ 10.00, as shown in figure 3.
Figure 3. Sensitivity analysis in the limit of pages
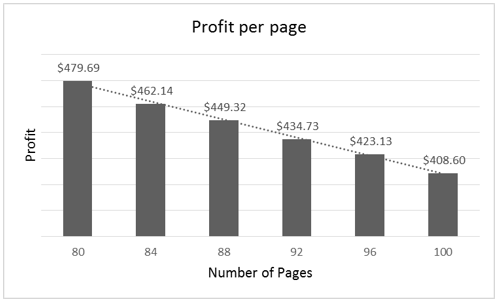
Source: The author(s)’ own.
Furthermore, it is possible to analyze the limit of advertisements that the salesman could sell. By decreasing and increasing the number of advertisements, it is possible to observe that, with the increase in the limit, the total profit has a significant increase and the profit per advertisement has a small decrease, as shown in figure 4. In addition, after 480 advertisements the total profit remains the same. Therefore, if one city has more than 480 companies, the optimal quantity to have the optimal total profit should be 480 advertisements.
Figure 4. Sensitivity analysis in the limit of advertisements
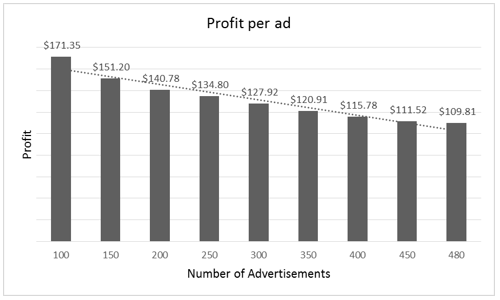
Source: The author(s)’ own.
Additionally, analyzing the percentage of small advertisements policy and the percentage of big advertisements policy it is possible to observe that they have a different reaction to the percentage increase. Figure 5 shows that, even with the percentage increase in the small advertisements policy, the total profit remains the same. However, in figure 6, it is possible to observe that, with the increase of the percentage in the big advertisements policy, the total profit decreased.
Figure 5. Sensitivity analysis in the small advertisements policy
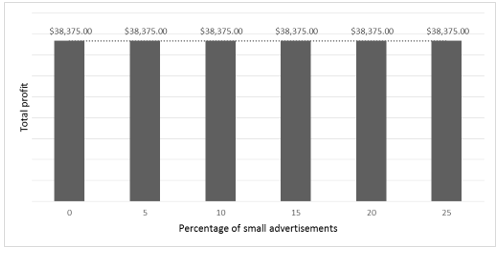
Source: The author(s)’ own.
Figure 6. Sensitivity analysis in the small advertisements policy
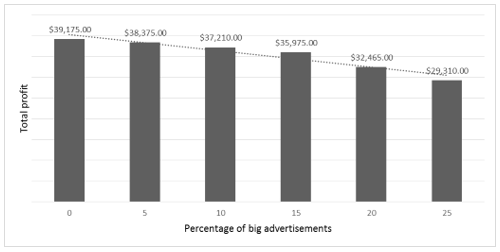
Source: The author(s)’ own.
4.4 Decision-Making
The Solver found an optimal solution that indicates that the optimal number of pages is 80, and the quantity of each size of advertisements is 15, 200, 5 and 80 for the size 1, size 3, size 4 and size 5, respectively. These optimal quantities leads to a total profit of $38,375.00.
Sensitivity analysis shows some information to improve or not the values of the problem. To increase the limit of pages that is possible to print, an investment in the printing machines and the change the design of the magazine would be necessary. Therefore, increasing the limit of pages is not interesting for the publishing house because the profit obtained with its increase is not significant enough.
In addition, the optimal number of advertisements that has the largest profit is 480. Therefore, it would be profitable if the salesman could find more than 300 advertisements per city; however, if the number of advertisements increased, it would be necessary to hire another salesman to visit the clients.
The data shows that the percentage of big advertisements influences the total profit while the percentage of small advertisements does not influence the total profit.
Analyzing this information, it is possible to define a strategy for the publishing house. The percentage of big and small advertisements should be kept, while the number of advertisements sold should be a number between 300 and 480, that is, the maximum that the salesman can sell without passing the limit of 480.
5 Conclusion
In conclusion, a publishing house has the objective of improving the process of producing magazines while maximizing the profit. To maximize its profit the magazine should have an optimal number of pages and the salesman should sell an optimal number of each advertisement. The problem about the optimal quantity of advertisements and pages for the publishing house may be solved through an operations research method. The model created to describe the problem is a linear programming with variables, objective function and constraints. The algorithm application led to an optimal solution and, with these quantities, it was possible to modify the constraints in order to test different realities to observe profit increases and decreases. The results of the algorithm application and the scenarios simulated incorporated important information about the selling process, and the existing policies and through decision-making, it is possible to improve the total profit.
References
Boskamp, V. et al. (2011), “Maximizing revenue with allocation of multiple advertisements on a Web banner”, Computers & Operations Research, Vol.38 No.10, pp. 1412-24.
Christensen, J.; Bastien, C. (2015), Nonlinear optimization of vehicle safety structures: Modeling of structures subjected to large deformations, 1st ed., Butterworth-Heinemann, Oxford.
Dym, C. L. (2004), Principles of mathematical modeling, 2nd ed., Academic Press, Cambridge.
Kumar, S. et al. (2006), “Scheduling advertisements on a web page to maximize revenue”, European journal of operational research, Vol.173 No.3, pp. 1067-1089.
Marszałkowski, J.; Drozdowski, M. (2013), “Optimization of column width in website layout for advertisement fit”, European Journal of Operational Research, Vol.226, No.3, pp. 592-601.
Xing, Y. et al. (2013), “Operations research (OR) in service industries: a comprehensive review”, Systems Research and Behavioral Science, Vol.30 No.3, pp. 300-53.
Yang, X. S. (2013), “Optimization and metaheuristic algorithms in engineering”, in Yang, X. S. et al. (Ed.), Metaheuristic in Water Geotechnical and Transport Engineering, Elsevier, Waltham, pp.1-23.
Zakharova, E. M.; Minashina, I. K. (2015), “Review of multidimensional optimization methods”, Journal of Communications Technology & Electronics, Vol.60 No.6, pp. 625-36.
Received: Oct 15, 2017
Approved: Jan 12, 2018
DOI: 10.14488/BJOPM.2018.v15.n1.a7
How to cite: Medeiros, N. B.; Vidor, G. (2018), “Advertisement quantity optimization to maximize profit in a Publishing House”, Brazilian Journal of Operations & Production Management, Vol. 15, No. 1, pp. 68-77, available from: https://bjopm.emnuvens.com.br/bjopm/article/view/406 (access year month day).