Capacity coordination in hybrid make-to-stock/make-to-order contexts using an enhanced multi-stage model
Masoud Rabbani1, Sara Motevali Haghighi1, Hamed Farrokhi-Asl2, Neda Manavizadeh3
1 University of Tehran; 2 Iran University of Science & Technology; 3 KHATAM University
Abstract
One of the most attracting production systems that has recently been vastly explored by practitioners and academicians is hybrid make-to-stock/make-to-order. Having a hierarchical production planning structure considered, this paper develops a multi-stage model to cope with the operational decisions, including order acceptance/rejection, product lot sizing, overtime capacity planning, outsourcing, and due date setting. Moreover, the proposed framework also comprises providing alternative products for the coming orders in order to enhance service level of the firm to the customers. In order to validate the presented framework, it is applied in a real industrial case study and the obtained results approve validity of the proposed framework.
Keywords: Production Planning; Hybrid MTS/MTO; Capacity Coordination; Acceptance/Rejection; Lot Sizing; Supplier Selection; Outsourcing.
1 Introduction
Manufacturing companies adopt different policies in order to meet their demands, among which one of the most appealing ones is Make-To-Order (MTO). The MTO systems deliver a high variety of orders, especially more expensive ones which are generally customized. Therefore, the production planning concentrates on average response time, average order delay, delivery lead-time, due dates, etc. (Mu, 2001).
In contrast with the MTO systems, a Make-To-Stock (MTS) production system concentrates on the anticipation of future demands of customers. Therefore, deliverable items are processed in advance and stored in warehouses and after this, customers’ orders are satisfied with the finished goods, which are available in inventory. In MTS systems, decisions are mainly made upon measures of production line fill rate, demand forecasts, lot-sizing, average work-in-process (WIP), etc. (Olhager, 2003).
Although there are many research papers that have explicitly addressed pure MTO and pure MTS production planning issues, only a handful of instances are found in real industrial environment adopting fully MTS or MTO in practice (Soman et al., 2004). One of the production systems which have recently attracted academicians and practitioners is the hybrid MTS/MTO. This system benefits from both pure MTS and pure MTO systems. Hybrid MTS/MTO systems are used to make balance between two aforementioned systems. In these systems, a common section of the line is dedicated to operate MTS parts of distinct products and the remaining section of the line is used to customize the in-process inventories upon the coming orders.
One of the most efficient approaches applied to the MTS/MTO production planning is the Hierarchical Production Planning (HPP), because this approach divides the involved decisions to some different decision-making levels, resulting at a less sophisticated decision environment. In the field of production planning, this method was introduced by Hax et Meal (1975). Soman et al. (2004) utilized the HPP method with three decision levels (strategic, tactical, and operational) in a system which has both MTS and MTO goods.
In the first level, the hierarchy consists of three main decisions. The First one was about forming product families, and then production systems of the product families and their Order Penetration Point (OPP - the point of the production line at which a specific order enters the production process) locations are specified (this level is called MTS/MTO decision). The second level namely capacity coordination, is designated to assigning capacity to MTS, MTO and hybrid orders. In this level, profitable MTO and hybrid orders are accepted and their due dates are specified; while other orders that are not profitable are rejected. Moreover, increasing the level of capacity is determined in order to meet customer orders, as well as determining lot sizes for the MTS predicted orders. In other words, it is decided how much capacity is assigned to the orders (by accepting some coming orders) and how much capacity is allocated to the stock-based production (by determining the lot sizes of the MTS products). Finally, the last level, that is, the scheduling and controlling level, determines the sequence of the products and details of production plan for the shop in order to meet due dates and lot sizes that were obtained in the previous level.
The most challenging level of the mentioned HPP might be the second level in which appropriate production capacities are devoted to distinct kinds of products upon accepted orders. Therefore, this level influences directly on very important performance measures of the corporations, such as profitability, customer loyalty, and reputation. Moreover, diverse decisions are decided in order to cover the second level of the HPP, which make the problem more sophisticated in the case of hybrid systems with the conflicting nature of the MTS and MTO sections of the production line.
This paper addresses the capacity coordination problem for the hybrid production systems with three kinds of products; pure MTS, pure MTO, and hybrid MTS/MTO. The considered problem belongs to the second level of the above-mentioned HPP; in other words, the problem is a tactical issue of the HPP. In this regard, it is decided to develop a multi-stage model in order to cope with all the decisions involved in the capacity coordination. Moreover, it is noted that an integrated model which is capable of coping with all the decisions of the capacity coordination might be a very complex model. Obviously, such a model is too difficult to be comprehended by the firm’s managers as well as model users.
The considered capacity coordination model comprises MTO and MTS/MTO orders acceptance/ rejection, MTS and MTS/MTO product family lot sizing, determining required overtime capacity and outsourcing, determining new prices and due dates for MTS/MTO orders in negotiation with the customers, and selecting suppliers for the outsourced MTS/MTO orders; among which the most notable decision of the developed model is the one relevant to acceptance/rejection of the coming orders. In the developed model, if the coming order is not feasible upon unfinished inventory at the OPP, this model proposes three ways for accepting orders: outsourcing, determining new price and proposing new due date for the coming order. Finally, and in the case of outsourcing, suppliers are selected to procure the outsourced items for the accepted orders.
The paper is organized as follows. Next section reviews the related literature. In Section 3, the proposed model, in which all modules and parts of the proposed structure are elaborated, is described. Additionally, validity and applicability of the proposed model is described through a real industrial case study in Section 4. Finally, conclusions and suggestions for future research are provided in Section 5.
2 Literature review
Although numerous instances of hybrid MTS/MTO production systems are found in real industrial environment, only a small number of research papers have been published so far in this research direction. In this regard, Williams (1984) was the first researcher who addressed hybrid production systems by analyzing the relationship between production capacity and customer demands in a single-station production facility using queuing theory. Next papers are categorized into two main groups, including quantitative and qualitative ones among which a former category includes some instances focusing on operational issues of hybrid systems. For instance, Adan et van der Wal (1998) analyzed the effects of adding MTO products to an MTS line on the system lead time. Kogan et al. (1998) addressed aggregate production planning of a multi-stage capacitated MTS/MTO production system upon inventory dynamisms of raw materials, unfinished and finished products. Beemsterboer et al. (2016) investigate the advantages of a hybrid planning method without considering a priority for either MTO or MTS. They developed a Markov Decision Process model for a two-product hybrid system to specify when to produce MTS and MTO products. Soman et al. (2007) optimized economic lot scheduling of a single-stage facility processing MTS, MTO, and hybrid MTS/MTO products. An order selection model was proposed by Ashayeri et Selen (2001), so as to maximize total contribution in a pigment manufacturing case. To do this, the authors developed a user interface for the marketing and manufacturing department of the case company. Similarly, Dobson et Yano (2002) addressed system selection in a single-stage production shop floor for a monopolist, whose demands declined as price and lead time increased. Another sample from the quantitative approaches is related to the paper by Maruf (2016) in which he presents a Base-Stock Control System (BSCS) model to categorize each incoming orders into the MTS and MTO. Each order is classified into the categories of High Volume (HV) and Low Volume (LV). All products in these two categories will be scheduled, using two alternative approaches, the First-In-First-Out (FIFO) and Priority Rule (PR).
On the other hand, qualitative research is formed in some papers that challenged the relevant issues of hybrid systems. For example, Ari Samadhi et Hoang (1995) considered a shared computer-integrated cellular manufacturing system between some manufacturers that adopted the MTS, MTO, Engineer-To-Order (ETO), and Assemble-To-Order (ATO) strategies. Upon the features of the mentioned systems, the authors provided implementation guidelines of the shared system in every four adopted production strategy. Moreover, Huiskonen et al. (2003) developed a model to choose proper inventory system of every product (MTS and MTO) upon sales volume and variance to enhance delivery lead time. Among the qualitative models, some models have been developed upon the concepts of HPP. In this regard, the first model was developed by Soman et al. (2004) as described in Section 1. Afterwards, three research papers were published by Zaerpour et al. (2009) and Gharehgozli et al. (2008) towards order partitioning in hybrid MTS/MTO and MTO production systems, respectively. Also, Ebadian et al. (2009) addressed acceptance/rejection procedure of MTO orders. However, the two most similar papers, compared to this paper, are the ones by Kalantari et al. (2011), Rafiei et Rabbani (2012), and Kuo et al. (2016). In the developed model by Kalantari et al. (2011), customers were prioritized upon some measures, using two methods AHP and fuzzy TOPSIS, and production capacities were assigned upon the prioritization results. They also developed a mathematical model to match the orders with the unfinished inventories. Some issues are notable about the model of Kalantari et al. (2011); the proposed matching model worked upon the order forecasts, while it is not acceptable about the coming orders with specific customization to be forecasted (the matching process is considered in make-to-forecast production environment). They assumed all coming orders are negotiable, while it is not the case in the real-world industrial contexts. Finally, they conducted numerical experiments on the developed mathematical model without any report on how the developed model worked totally. Rafiei et Rabbani (2012) modeled the second level of the HPP in hybrid MTS/MTO production systems including three kinds of products: pure MTS, pure MTO and the hybrid MTS/MTO. They proposed a mathematical model for determining the lot-sizes of MTS and MTS/MTO products before their relevant OPPs. Also, they proposed a procedure for acceptance/rejection of the coming MTO and MTS/MTO orders.
Concluding the literature, more exploration is required to be performed on the second level of HPP in hybrid MTS/MTO manufacturing systems, since this level focuses on the capacity issues as well as the acceptance/rejection procedures. In this regard, this paper extends the model presented by Rafiei et Rabbani (2012). The developed model of this paper adds three features to that of Rafiei et Rabbani, by determining level of outsourcing, negotiating new prices and new due dates for the coming negotiable orders, and selecting the best suppliers for the outsourced orders. In the developed structure, if the coming order is not feasible upon unfinished inventory at the OPP, three alternatives are considered for accepting the orders: outsourcing, determining new price, and proposing new a due date for the coming order. Additionally, selecting suppliers for the outsourced orders is augmented to the proposed structure.
3 Proposed model
In this section, the developed multi-stage capacity coordination model is described in detail. In this regard, the proposed model is categorized into three parts. The first one, product families, is obtained from different orders that are received from the customers. Second, decisions are made on which production system each product family follows and; third, the OPP locations of the MTS/MTO product families are specified. MTO product families are disconnected from other product families, because MTS and MTS/MTO product families are operated based on predictions. In these separated product families, they are sorted, for the reason that the model is presented to accept the most favorable MTO families. On the other hand, production values of MTS and MTS/MTO product families are evaluated to consider the qualitative criteria in the proposed lot-sizing module. After sorting MTO orders and evaluating qualitative criteria for MTS and MTS/MTO products, capacity allocation is determined. In this regard, MTO families are addressed initially, since their importance is higher than MTS and MTS/MTO products (Huiskonen et al., 2003). Thus, an initial capacity is allocated to MTO families. To do this, expected values of required capacities to produce high-priority MTO orders are assigned, since high-priority MTO orders are the orders that should be accepted (Ebadian et al. 2008). Next, lot sizes of other two categories of products (MTS and MTS/MTO) are calculated, because their demands are forecasted. It is noted that forecasted demands (MTS and MTS/MTO products) are not first responded, as the acceptance of all coming high-priority MTO orders is required. After lot-sizing, the available capacity equals the sum of the initially assigned capacity and the remained capacity from lot-sizing. On the other hand, MTS/MTO families are afterwards in their MTO-based production activities. Hence, acceptance/rejection is performed for MTO and MTS/MTO product families with respect to the available capacity. In this step, MTS/MTO priorities and OPPs are taken into account in order to decide on acceptance/rejection. Simultaneously, due-date setting is performed, because due date plays a key role in accepting or rejecting orders. By means of the proposed model, capacity is balanced between MTS products and high-priority MTO and MTS/MTO orders. To do so, the required capacity is first devoted to high-priority orders and then lot-sizing is performed for the forecasted demands. Next, decisions on coming orders are made upon the available capacity for these orders. The proposed model is developed for production systems with MTS, MTO and MTS/MTO product families, whilst the layout of the system is assumed as job-shop, in which arriving orders have specific process routes. Figure 1 shows the proposed capacity coordination model. The following sections explain the modules of the proposed capacity coordination model.
Figure 1. The proposed capacity coordination model
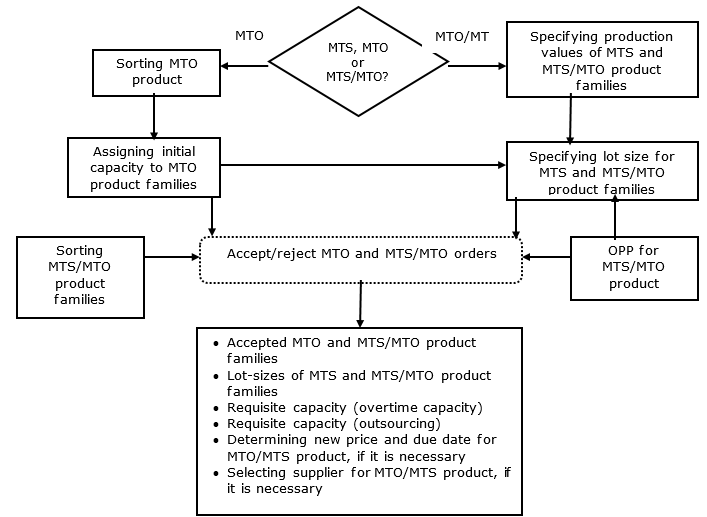
Source: The author(s)
3.1 Prioritizing MTO product families
In this section, four criteria are described to prioritize the coming MTO orders. It is noted that the receiving orders are from the product families which the firm is capable to process and deliver. Hence, the term “product families” is used. These criteria are related to MTO customers. The criteria are customer’s profit contribution, customer’s potential purchasing, orders’ lot sizes, and orders’ purchasing range. The values that are assigned to the criteria are “Low” and “High”. Based upon different combinations of the criteria, Table 1 demonstrates corresponding order priority of every combination (Rafiei et Rabbani, 2012). As seen in Table 1, the impossible combinations are not listed. For example, combination (L, L, H, L) is not applicable, because it is impossible to have a large lot size and low profit contribution and potential purchasing.
Table 1. Prioritization of MTO product families.
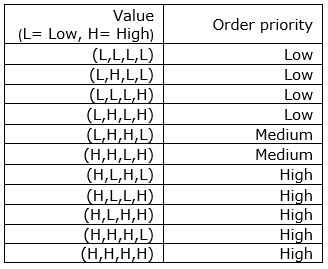
Source: The author(s)
3.2 Determining production values of MTS and MTS/MTO product families
Three criteria including estimated contribution, reputation, and potential future sale are considered for determining production values of MTS and MTS/MTO product families. To do so, production values are calculated as the weighted sum of normalized values regarding the three criteria mentioned above. Since the considered criteria are qualitative, their relevant values are determined through experimental judgments of the production and marketing staff.
3.3 Assigning initial capacity to MTO product families
Initial capacities are allocated to High-Priority MTO (HPMTO) product families, because these types of product must be delivered on-time. Hence, expected required capacity of future coming HPMTO orders are calculated as follows:
Expected capacity of resource j for HPMTO = ∑ (Acceptance probability of order i × required capacity of order i in resource j)
Where order i belongs to the HPMTO that is determined in Section 3.1 and resource j belongs to the process route of order i (jϵR(i)). Also, the acceptance probability is calculated using (1).
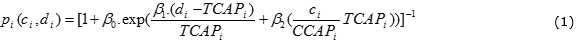
In above statement, parameters are used as:

It is noted that Equation (1) is obtained upon Berkson’s binary choice logit model in which coefficients 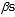 are estimated empirically from previous data of the previous orders of the firm. Moreover, using a log transformation, the coefficients are obtained, using the least square regression model. In this regard, a comprehensive study is conducted by Easton et Moodie (1999), to which eager readers are referred. Therefore, the initial capacity of resource j that is allocated to the HPMTO orders is (
are estimated empirically from previous data of the previous orders of the firm. Moreover, using a log transformation, the coefficients are obtained, using the least square regression model. In this regard, a comprehensive study is conducted by Easton et Moodie (1999), to which eager readers are referred. Therefore, the initial capacity of resource j that is allocated to the HPMTO orders is (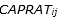 is processing time of product family i in resource j):
is processing time of product family i in resource j):
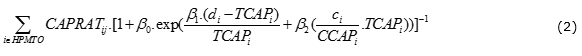
3.4 Determining lot sizes for MTS and MTS/MTO product families
When the initial capacity is allocated to HPMTO product families, the remained capacity is free to plan for MTS and MTS/MTO product families, for which lot sizes are optimized, since there are setups to produce the products. To do so, Equations (3)-(13) are proposed to minimize the total costs of manufacturing resources and warehousing capacity constraints. Moreover, it is noted that the regular-time capacity considered in this model is the remained capacity calculated from the allocated capacities, i.e. total available capacity minus the initially allocated capacities to the MTO product families.

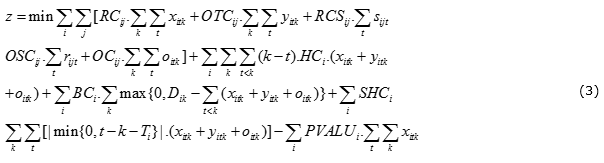

Objective function (3) minimizes total production, setup, holding, backlog and outsourcing costs. Furthermore, the penalty cost for perishable product families is considered in the objective function, while the last term of the objective function seeks to maximize production value of all product families which are processed in regular time. It is noted that the perishability cost is considered separated from the holding costs of product families, since it has a distinct nature from the holding cost. Moreover, holding cost is inevitable for all product families; however, there is not any perishability concern in terms of some product families. Maximum outsourcing is taken in Constraints (4), while Constraints (5) and (6) correspond to the setups in regular time and overtime, respectively. Available regular-time and overtime resource capacities are taken into account in (7) and (8), respectively. The warehousing capacity is also considered using (9). Constraints (10) are related to the demand balance. Finally, Constraints (11) and (12) define the required variables.
3.5 Accepting/ rejecting MTO and MTS/MTO orders
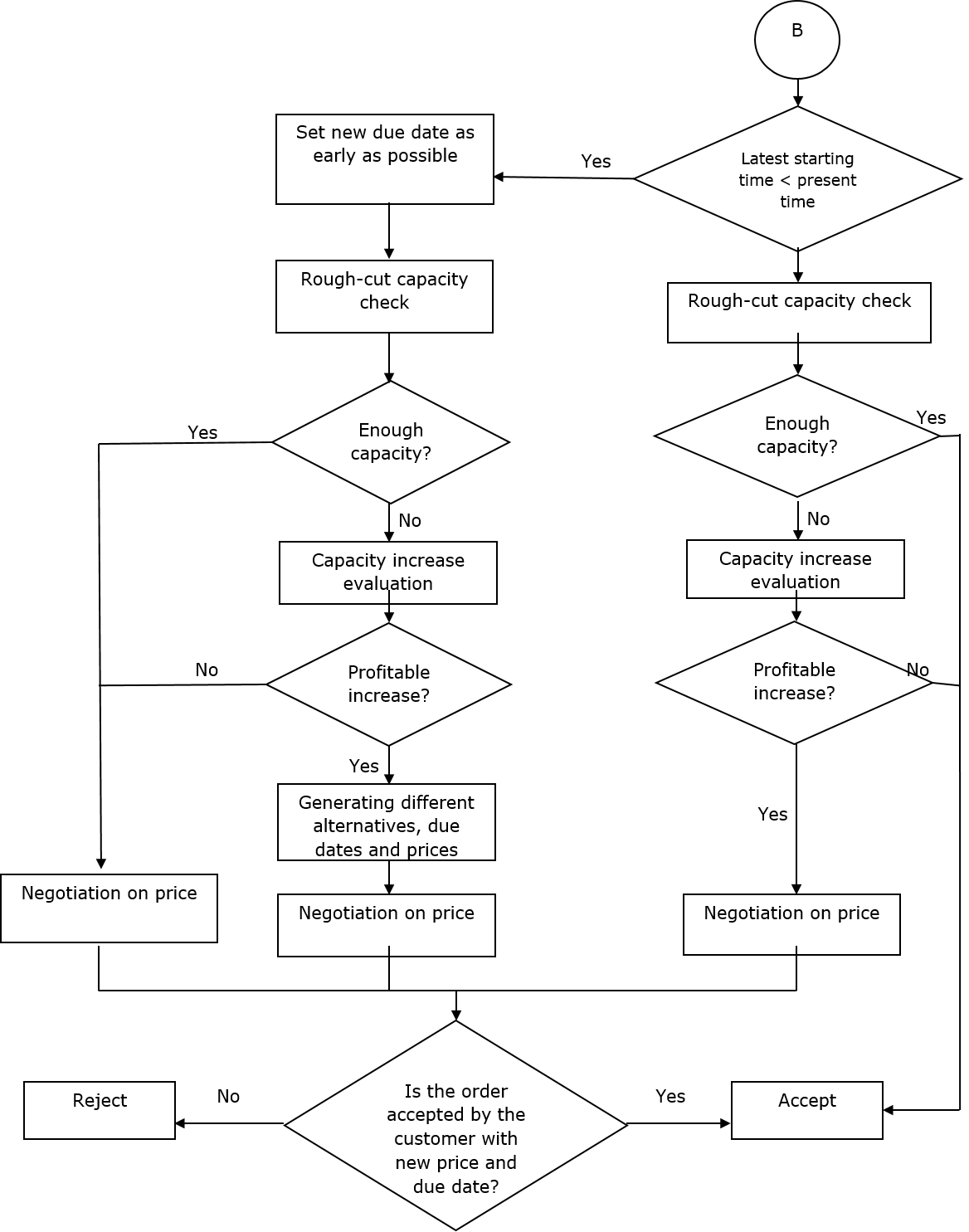
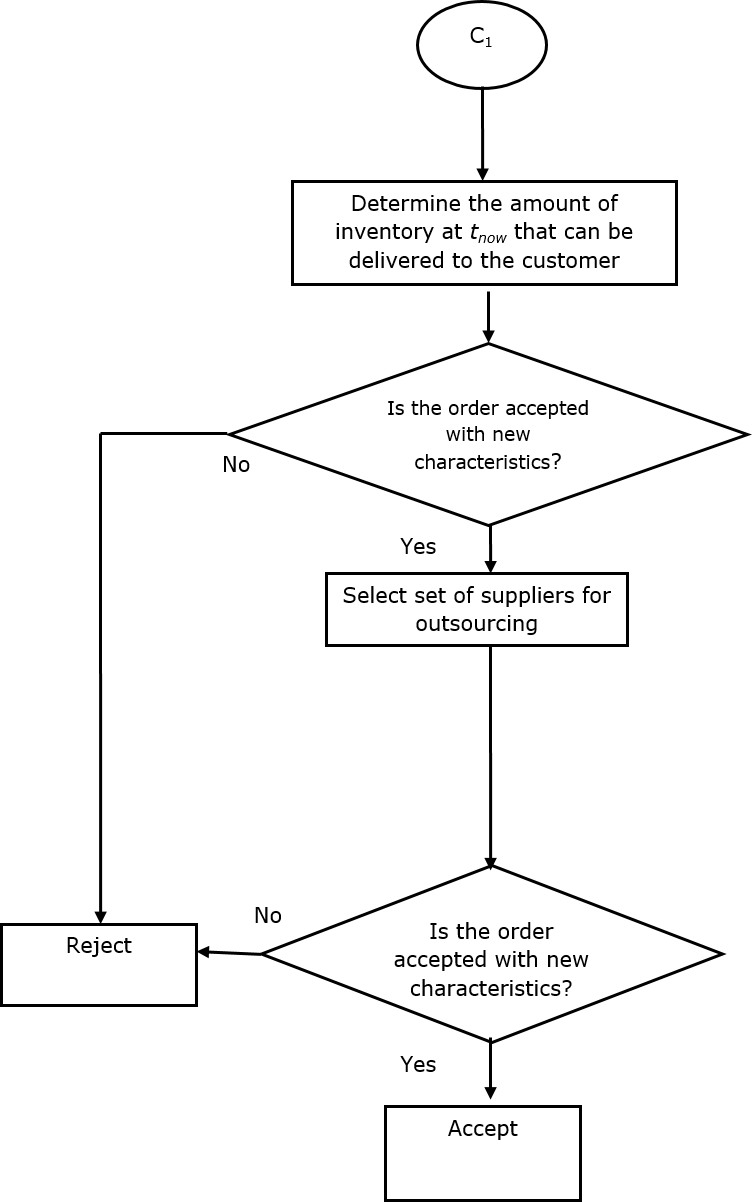
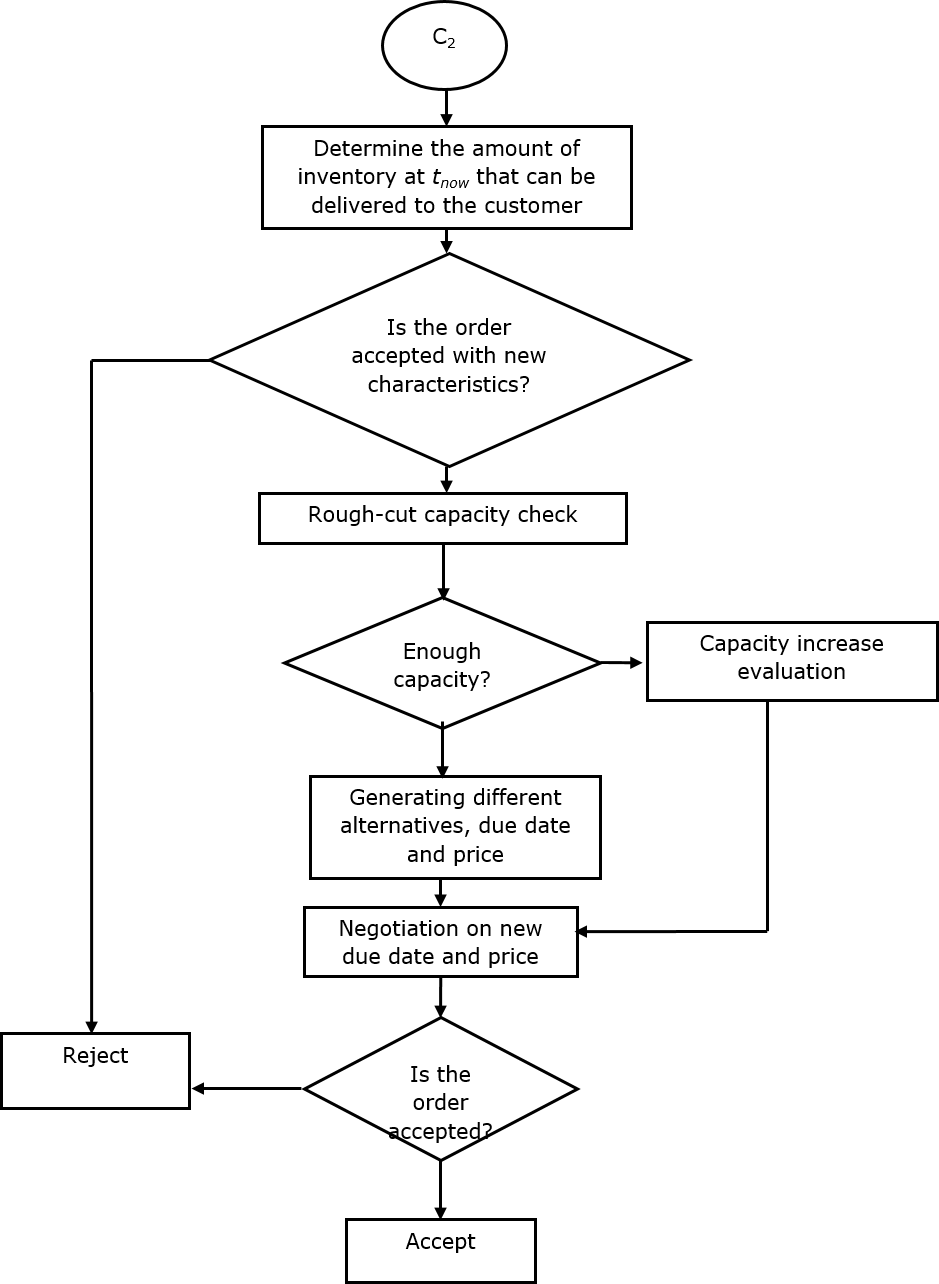
In this step, profitable MTO orders are distinguished to be accepted and the ones that do not yield our desired level of profitability will be rejected. In this procedure, negotiable orders are separated from the non-negotiable ones for the MTO product families; also, three priority levels of the orders are considered: high priory, medium priory and low priory (Figure 2 shows the developed acceptance/rejection procedure). The proposed acceptance/rejection structures for non-negotiable and negotiable orders are presented in Structures A (Figure 2(b)) and B (Figure 2(c)), respectively. Figure 2.3(d) demonstrates Structure C1, which corresponds to the outsourcing option of the orders, while Figure 2.3(e), Structure C2, presents the procedure to negotiate on different prices and lead times for the negotiable orders. Figure 2.3(f), Structure C3, describes substitutability of similar orders to be delivered to customers.
Figure 2(a). Proposed module toward MTO and MTS/MTO acceptance/rejection
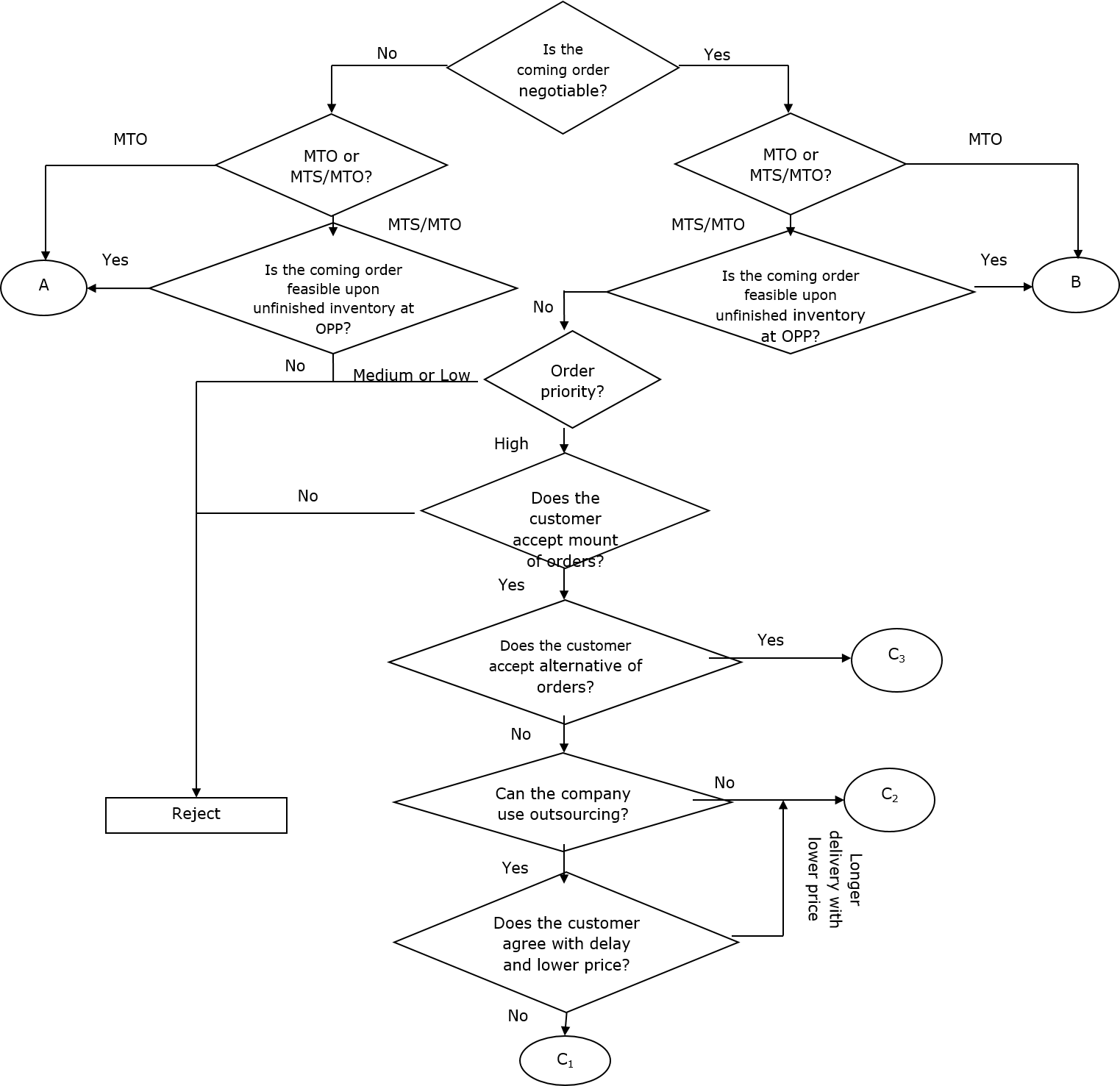
Source: The author(s)
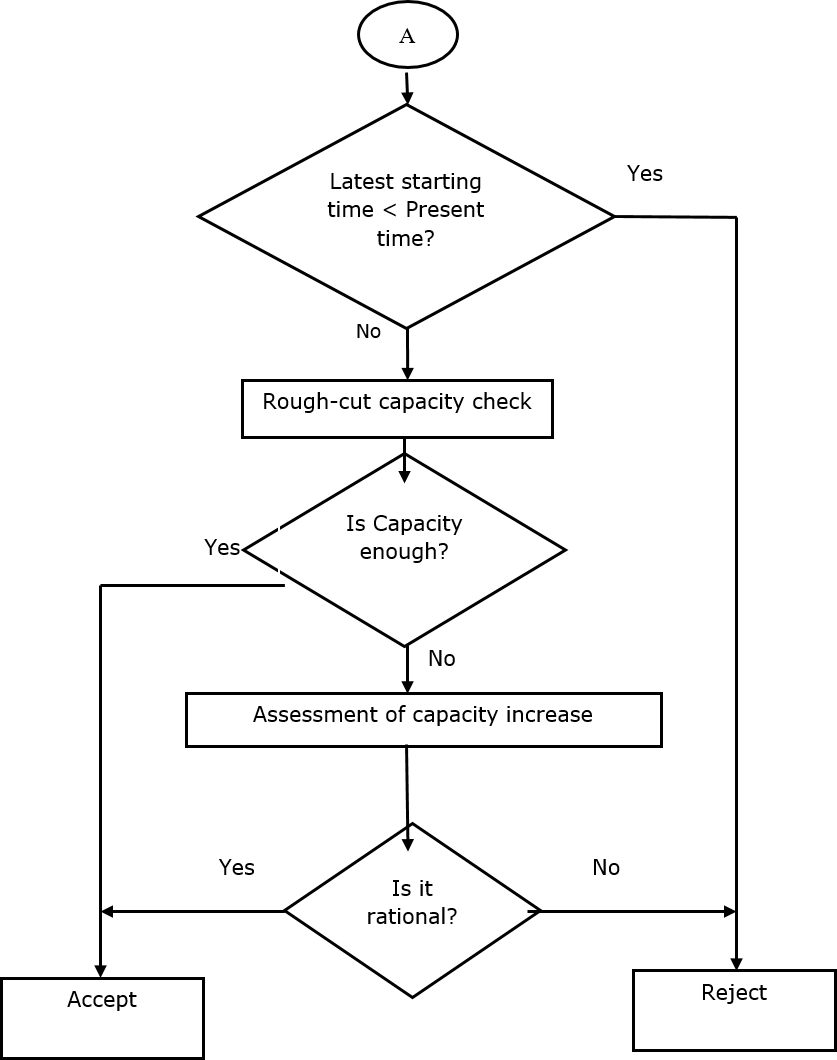
Figure 2(b). Proposed module toward MTO and MTS/MTO acceptance/rejection (cont’d)
Source: The author(s)
Figure 2(c). Proposed module toward MTO and MTS/MTO acceptance/rejection (cont’d)
Source: The author(s)
Figure 2(d). Proposed module toward MTO and MTS/MTO acceptance/rejection (cont’d)
Source: The author(s)
Figure 2(e). Proposed module toward MTO and MTS/MTO acceptance/rejection (cont’d)
Source: The author(s)
Figure 2(f). Proposed module toward MTO and MTS/MTO acceptance/rejection
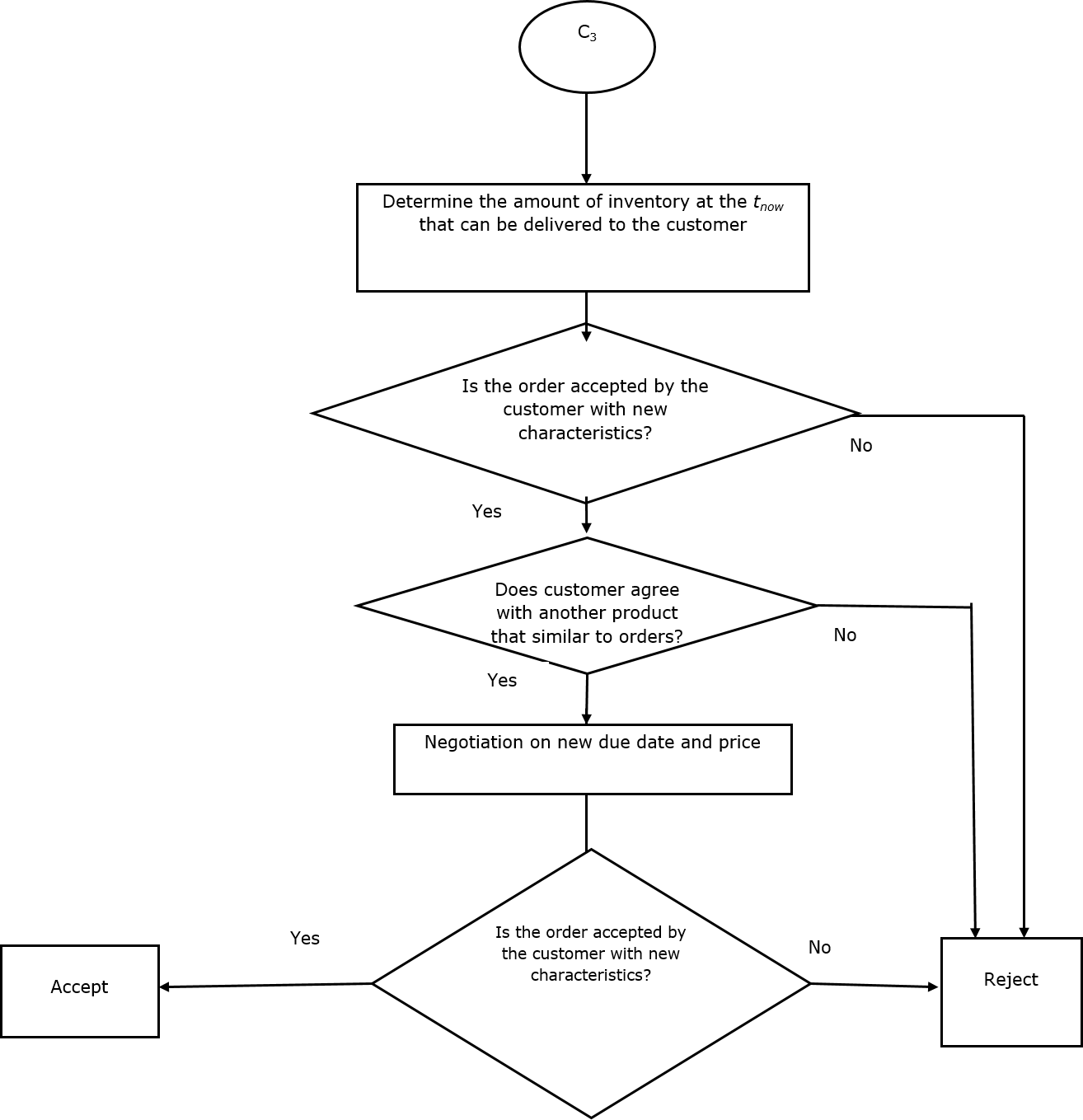
Source: The author(s)
3.5.1 Calculating the latest stating time
Latest Starting Time (LST) is calculated for any order. The following equation, Equation (13), is used to calculate LST:

3.5.2 Determining the amount of deliverable inventory at tnow to the customer
To check unfinished inventory for the coming orders, the following constraints (Constraints (14)-(16)) are utilized to check the feasibility of high-priority, medium-priority, and low-priority orders, respectively. With respect to the following constraints, the amount of inventory at 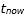 that can be delivered to the customer is determined [24].
that can be delivered to the customer is determined [24]. 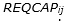 is the required capacity of resource j for production of order i, while
is the required capacity of resource j for production of order i, while 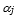 and
and 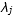 are the percentage of the resource j capacity that remains unfilled for high-priority and medium priority orders, receiving later than period t, respectively, which are determined by the production experts of the firm.
are the percentage of the resource j capacity that remains unfilled for high-priority and medium priority orders, receiving later than period t, respectively, which are determined by the production experts of the firm.
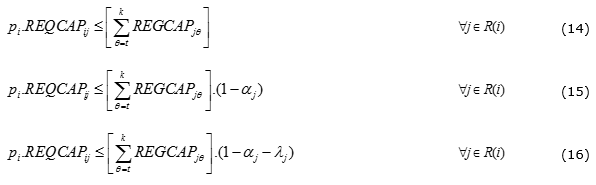
Using the above constraints, a rough-cut capacity check is also performed.
3.5.3 Evaluating capacity increase
In this step, profitability of the increasing capacity is evaluated. To do so, the cost of capacity increase is compared with the gained margin of the capacity increase. If the margin is greater than the cost, increasing capacity is profitable and the order is accepted; otherwise, the order is rejected.
3.5.4 Selecting set of suppliers for outsourced orders
According to the acceptance/ rejection procedure presented in Figure 2, the following mathematical model is developed in order to select suitable suppliers for the outsourced items decided in the model of Section 3.4.


Objective function (17) minimizes the total cost of suppliers and subcontractors, raw material lateness and earliness in regular time and overtime. Constraints (18) and (19) consider capacity of resource r in regular time and overtime, respectively. Workload relations are presented in (20)-(23); whilst it is required to select one supplier and one subcontractor using Constraints (24) and (25), respectively. Constraints (26) define the decision variables.
4 Case study
In this section, an industrial case study is reported to validate the applicability and validity of the proposed model. The reported case study relates to a wood-industry manufacturing company in Iran, which is one of the most leading firms in the Iranian and Western Asian markets. The company is called Company X in this section. It should be noted that, for the reason of confidentiality issues, the company did not permit us to present all the related data to the case; however, it is attempted to present the data that are necessary to reproduce the results in future research. This company had some problems, such as long lead times, which resulted in many cases whose promised due dates had not been met. Also, high holding and backlog costs persuaded the managers of the company to treat the problems. Therefore, the authors decided to restructure the production planning procedures of the company. The main reported problems were related to the decisions in the domain of capacity coordination (high holding cost, high overtime cost, delivering orders with delay, unfinished inventory shortage, etc.). To do so, it was decided to concentrate on the capacity coordination issues of Company X. This firm has nine product families from which three families are MTS (e.g. furniture), three families are MTO (e.g. door) and the last three families are MTS/MTO (e.g. decoration). These products are processed through different process routes, using 19 workstations. Table 2 contains data about processing time periods of the product families in workstations. The numbers in parentheses correspond to setup time periods (setup time periods in regular time are as the same as those of overtime). Moreover, production cost per unit of regular time, production cost per unit of overtime, setup cost per unit of time (both regular time and overtime), and outsourcing cost are 15, 20, 25, and 28 respectively.
Table 2. Data about processing time periods of product families (setup time periods are in parentheses)

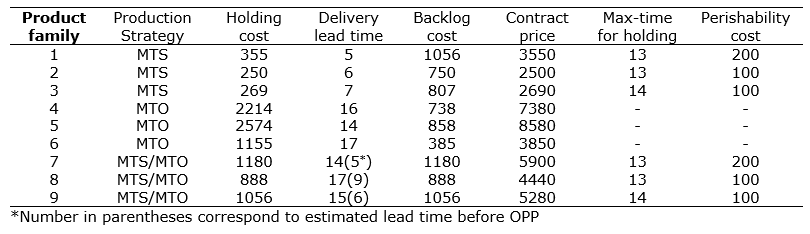
In Table 3, data of the product families are presented; contract prices are approximately %130 of total cost (sum of processing and setup costs), while holding and backlog costs are %10 and %30 of MTS prices, %30 and %10 of MTO prices and %20 and %20 of MTS/MTO prices, respectively. Also, it is noted that the planning horizon is one month, which includes 4 weeks ×5 days ×7 hours× 60 minutes= 8400 minutes regular time and 4 weeks ×4 days ×2 hours× 60 minutes = 1900 minutes as overtime (overtime is allowed on Monday, Tuesday, Wednesday and Thursday).
Table 3. Data of the product families
Source: The author(s)
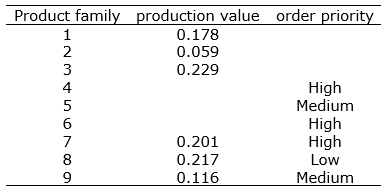
According to the developed methods in Sections 3.1 and 3.2, production values and order priorities are resulted upon the judgments of the firm evaluations as in Table 4.
Table 4. Production values and priorities of product families.
Source: The author(s)
In the next step, initial capacity for HPMTO orders is calculated, parameters 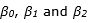 were set at 0.1, 0.5, and 0.75 based upon the historical data from the customer. To do so, Formula (1) was transformed to logarithmic form upon which parameters
were set at 0.1, 0.5, and 0.75 based upon the historical data from the customer. To do so, Formula (1) was transformed to logarithmic form upon which parameters 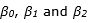 were the coefficients of the transformed formula. To estimate the coefficients, a regression model was done using Microsoft Excel® spreadsheets. Then, the obtained parameters were modified by the firm experts.
were the coefficients of the transformed formula. To estimate the coefficients, a regression model was done using Microsoft Excel® spreadsheets. Then, the obtained parameters were modified by the firm experts. 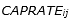 was assumed as the sum of the total processing and setup time periods of product family i in resource j. Moreover,
was assumed as the sum of the total processing and setup time periods of product family i in resource j. Moreover, 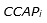 was equal to the average of production cost in regular time, production cost in overtime and setup cost; i.e.
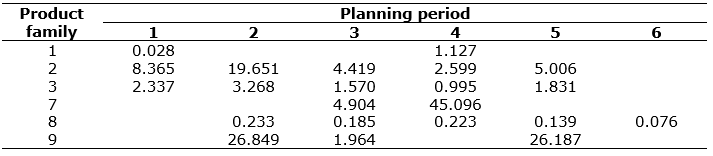
was equal to the average of production cost in regular time, production cost in overtime and setup cost; i.e. 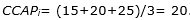 . Thus, the acceptance probabilities of product families 4, 5, 6, 7, 8, and 9 were calculated as 0.85, 0.92, 0.88, 0.93, 0.93, and 0.93; furthermore, lot sizes of MTS and MTS/MTO product families, as well as their outsourced volumes, were calculated in this step using the proposed mathematical model solved by GAMS 22.1\ DICOPT in nearly one and a half hour (90 minutes). It is noted that the size of the problem (9 product families within 19 resources during 20 working days) was globally optimized by the coded program in the software package; otherwise, some inexact algorithms should have been developed for the developed mathematical model. Results are shown in Tables 5 and 6.
. Thus, the acceptance probabilities of product families 4, 5, 6, 7, 8, and 9 were calculated as 0.85, 0.92, 0.88, 0.93, 0.93, and 0.93; furthermore, lot sizes of MTS and MTS/MTO product families, as well as their outsourced volumes, were calculated in this step using the proposed mathematical model solved by GAMS 22.1\ DICOPT in nearly one and a half hour (90 minutes). It is noted that the size of the problem (9 product families within 19 resources during 20 working days) was globally optimized by the coded program in the software package; otherwise, some inexact algorithms should have been developed for the developed mathematical model. Results are shown in Tables 5 and 6.
Table 5. Lot sizes of the product families within each planning period in regular time.

Source: The author(s)
Table 6. Outsourcing of the product families within each planning period.
Source: The author(s)
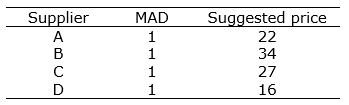
With respect to the subcontracted values and selected suppliers, results of an instance are presented for the sake of confidentiality. In this regard, Product family 2 in Period 2 is considered with the obtained amount of 19.651. The utilized resources for the production of Product family 2 were Resources 1, 4, 7, 11, 17, 18, and 19 for which suitable subcontractors were decided using the proposed model in Section 3.5.4 with the results presented in Table 7. In this table, the selected subcontractors are called p and q. Moreover, suitable suppliers for Product family 2 were selected to deliver the relevant raw materials in Period 1 with the optimal prices. The results are presented in Table 8 (earliness and lateness penalties were considered 18). The resulted solutions were obtained using software package GAMS 22.1\ DICOPT within 196 minutes (more than three hours) optimally.
Table 7. Subcontracted resources and suggested prices.

Source: The author(s)
Table 8. Selected suppliers with their relevant suggested unit prices
Source: The author(s)
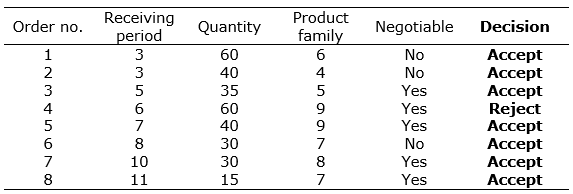
Finally, the proposed procedure for order acceptance/rejection was performed during twenty working days of the planning horizon. With regard to the eight received orders, suitable decisions for these orders are presented in Table 9.
Table 9. Summary of the acceptance/rejection decisions
Source: The author(s)
Having the proposed model applied in Company X, the above-mentioned results were obtained upon which a comparison is conducted between the company’s performance before and after the application of the proposed model. In this regard, the results of Table 10 are attained with respect to the comparison criteria in Rafiei et Rabbani (2012).
Table 10. Summary of the acceptance/rejection decisions

Source: The author(s)
5 Conclusion remarks and future research directions
Since the introduction of the HPP approach into the MTS/MTO production systems, diverse research papers have been published, among which the second-level (tactical) decisions are rarely focused. Among the tactical decisions, capacity coordination might be the most challenging one, since it covers several conflicting decisions related to the different natures of the MTS and MTO processes. Moreover, this level plays a key role in system performance due to direct effects on profitability, customer loyalty, and reputation. In this regard, a novel framework was proposed in this paper, which included different modules to make a decision in terms of order acceptance/rejection, product lot sizes, overtime capacity planning, outsourcing capacity planning and due date setting. Additionally, this paper added three new features to the models in the literature body by quoting new prices and due dates during negotiation with customers, providing alternative and outsourced orders, and selecting suppliers for the outsourced orders. The results of the proposed framework were studied in a real case study. The obtained results demonstrated that the proposed structure resulted in lower levels of delayed order deliveries, more due date adherence and lower overtime cost, whilst number of setups is increased.
To continue the research direction of this paper, recommendations are fourfold. First, it seems too practical to the proposed framework to form a complete there-level hierarchical decision structure in hybrid MTS/MTO. In such a structure, levels are correspondent to strategic, tactical and operational decisions, whose inputs and outputs are linked to each other upon a hierarchical structure. Moreover, capacity planning, using stochastic processes, might be technically sound. Upon the findings of this approach, sensitivity analyses of the decision parameters are useful. Also, developing and linearizing the proposed mathematical models in this paper might be helpful to have better model structure, leading to easier models to solve. Finally, the fourth recommendation is to study coordination in other types of production systems, such as engineer-to-order, assemble-to-order, or make-to-forecast, since the potential results of these systems might be meaningful in practice.
References
Adan, I. J., and Van der Wal, J. (1998). Combining make to order and make to stock. Operations-Research-Spektrum, Vol. 20, No. 2, pp. 73-81.
Ari Samadhi, T. M. A., and Hoang, K. (1995). Shared computer-integrated manufacturing for various types of production environment. International Journal of Operations & Production Management, Vol. 15, No. 5, pp. 95-108.
Ashayeri, J., and Selen, W. J. (2001). Order selection optimization in hybrid make-to-order and make-to-stock markets. Journal of the Operational Research Society, Vol. 52, No. 10, pp. 1098-1106.
Beemsterboer, B., Land, M., Teunter, R. (2016). Hybrid MTO-MTS production planning: An explorative study. European Journal of Operational Research, Vol. 248, No. 2, pp. 453-461.
Dobson, G., and Yano, C. A. (2002). Product offering, pricing, and make‐to‐stock/make‐to‐order decisions with shared capacity. Production and Operations Management, Vol. 11, No. 3, pp. 293-312.
Easton, F. F., and Moodie, D. R. (1999). Pricing and lead time decisions for make-to-order firms with contingent orders. European Journal of operational research, Vol. 116, No. 2, pp. 305-318.
Ebadian, M., Rabbani, M., Jolai, F. et al. (2008). A new decision-making structure for the order entry stage in make-to-order environments. International Journal of Production Economics, Vol. 111, No. 2, pp. 351-367.
Ebadian, M., Rabbani, M., Torabi, S. A. et al. (2009). Hierarchical production planning and scheduling in make-to-order environments: reaching short and reliable delivery dates. International Journal of Production Research, vol. 47, No. 20, pp. 5761-5789.
Gharehgozli, A. H., Rabbani, M., Zaerpour, N. et al. (2008). A comprehensive decision-making structure for acceptance/rejection of incoming orders in make-to-order environments. The International Journal of Advanced Manufacturing Technology, Vol. 39, No. 9-10, pp. 1016-1032.
Hax, A. C. and Meal, H. C. (1973). Hierarchical integration of production planning and scheduling. Boston, MA: Massachusetts Institute of Technology, Operations Research Center.
Huiskonen, J., Niemi, P. and Pirttilä, T. (2003). An approach to link customer characteristics to inventory decision making. International Journal of Production Economics, Vol. 81, pp. 255-264.
Kalantari, M., Rabbani, M. and Ebadian, M. (2011). A decision support system for order acceptance/rejection in hybrid MTS/MTO production systems. Applied Mathematical Modelling, Vol. 35, No. 3, pp. 1363-1377.
Kogan, K., Khmelnitsky, E. and Maimon, O. (1998). Balancing facilities in aggregate production planning: make-to-order and make-to-stock environments. International Journal of Production Research, Vol. 36, No. 9, pp. 2585-2596.
Kuo, Y., Yang, T., Parker, D. et al. (2016). Integration of customer and supplier flexibility in a make-to-order industry. Industrial Management & Data Systems, Vol. 116, No. 2, pp. 213-235.
Maruf, A. (2016, February). Scheduling Method for MTS/MTO Production System. In IOP Conference Series: Materials Science and Engineering, Vol. 114, No. 1.
Mu, Y. (2001). Design of hybrid make-to-stock, make-to-order manufacturing system (Doctoral dissertation, MSc Thesis, University of Minnesota).
Olhager, J. (2003). Strategic positioning of the order penetration point.International journal of production economics, Vol. 85, No. 3, pp. 319-329.
Rafiei, H., and Rabbani, M. (2012). Capacity coordination in hybrid make-to-stock/make-to-order production environments. International Journal of Production Research, Vol. 50, No. 3, pp. 773-789.
Soman, C. A., Van Donk, D. P. and Gaalman, G. (2004). Combined make-to-order and make-to-stock in a food production system. International Journal of Production Economics, Vol. 90, No. 2, pp. 223-235.
Soman, C. A., Van Donk, D. P. and Gaalman, G. J. (2007). Capacitated planning and scheduling for combined make-to-order and make-to-stock production in the food industry: An illustrative case study. International Journal of Production Economics, Vol. 108, No. 1, pp. 191-199.
Williams, T. M. (1984). Special products and uncertainty in production/inventory systems. European Journal of Operational Research, Vol. 15, No. 1, pp. 46-54.
Zaerpour, N., Rabbani, M., Gharehgozli, A. H. et al. (2009). A comprehensive decision making structure for partitioning of make-to-order, make-to-stock and hybrid products. Soft Computing, Vol. 13, No. 11, pp. 1035-1054.