AHP-De Borda: a hybrid multicriteria ranking method

Helder Gomes Costa¹

1 Fluminense Federal University

Abstract

De Borda voting method was proposed in the period of French revolution to be used in a multiple decision-maker environment. Later, it was adapted to multicriteria ranking problems. The adoption of criteria weights in De Borda modeling is an evolution of the original De Borda method; despite this fact, evolution does not approach how to define the weights, that is: the weights are an input to De Borda. The proposal is to segment the problem into two ones. The first is a weight assignment problem and was approached through AHP modeling. The second problem is a ranking problem, being approached through De Borda method. AHP and De Borda are based in principles from different multicriteria Decision Schools: AHP is classified into the American School; De Borda is recognized as a French method. This paper shows that it is possible to use both methods, in a complementary way. The proposal can assist and support decision makers in the modeling of multicriteria ranking problems by assigning weights to the criteria under a systematized way. This hybrid approach proposes a better way for the structuring of the problem, by linking an approach that natively supports the assignment of weights (AHP) into another devoted to the ordering of objects (De Borda).

Keywords: Ranking; Analytic Hierarchy Process; Decision; Multicriteria.

1 Introduction

Decision under a complex environment has been studied in classical texts alike Arrow (1951), Fishburn (1964), Saaty (1980), Zeleny (1982), Changkong et Haimes (1983), and Roy et Boyssou (1985), that analyzed such problems under a multiple criteria perspective. Despite the advances already reached, this subject remains under evolution as one can see in recent works such as Figueira, Greco et Ehrgott (2005), Gomes, Gomes et Maranhão (2010), Costa (2011), Figueira et al. (2011), Almeida-Dias et al. (2012), Nepomuceno et Costa (2015), Sant'Anna, Costa et Pereira (2015) and Pereira et Costa (2015). In this context, the multi-criteria decision is characterized by modeling decision problems under multiple points of view, whether quantitative or subjective.

Roy & Boyssou (1985) took into account four decision situations:

Choice: the decision maker seeks to identify and select a limited set of alternatives. This situation is denoted by p. α (alpha). This problematic is also called in literature as the portfolio problem.
Sorting: the alternatives are grouped into categories that have a ranking order relationship as it occurs in like-Pareto ABC classifications. This situation is denoted by p. β (beta)
Ranking: the objective is to build a ranking of alternatives which seeks to build an ordered list of alternatives, from the best to the worst. This situation is denoted by Problematic p. γ (gamma)
Description: the purpose is to identify and describe the main characteristics that distinguish the alternatives. This situation is denoted by Problematic p. δ (delta).

As reported in H. G. Costa (2016), there are at least two other problematics: prioritization or sharing (here denoted by p.σ), and categorization (here denoted by p. θ):

Sharing: it deals with problems in which finite resources must be shared or distributed by a group of elements, as in a budget. It fits, for example, the decision-making situations in which one identifies the percentage of resources to be assigned to each alternative. In this type of classification the problem of assigning weights to criteria can also be categorized, upon which the decision-makers want to distribute importance among the criteria for a set of previously defined criteria. One should notice that it is a typical trade off problem with finite resources, where shifting the allocation to an alternative means that, at least, another one should reduce its participations in the solution. The P.σ complements the original categorization because it addresses a set of decision issues not yet covered therein, such as the project budget, market share, and cost sharing.
Categorization: it addresses problems in which one wishes to allocate similar alternatives into homogenous groups that can be discerned from each other but there is not any relationship of importance or preference between them. It covers such situations as health diagnostics (hypertension, coronary disease, diabetes, etc.) and categorizations of species of animals (vertebrates, invertebrates, mammals, amphibians, etc.). It differs from the sorting (P. β) problem, because in p.θ there are not preference relationships among the categories.

The method De Borda was first introduced to deals with voting problems and its algorithm is addressed to the problematic p.γ, once it performs a ranking of alternatives. There are variations of De Borda that uses criteria’s weights as input. In such situations, the weights are usually assigned using intuitively scales with five positions, or even score scales with scores varying from 0 to 10 or from 0 to 100 points. In these cases, it is not usual to employ a technique for validating the consistency of the weights. On the other hand, the AHP (Analytic Hierarchy Process, Saaty, 1977) actually deals in its background with a sharing problem.

Thus, the present work proposes a hybrid De Borda-AHP method, to deals with ranking problems in such a way that: AHP focuses on the elicitation of criteria’s weights that area applied as an input to De Borda ranking method. Notice that it is a hybrid approach and not a fusion of methods, since the problem is partitioned into two stages: in the first one, AHP is used, to generate the input for the second one, in which De Borda is adopted to establish the ranking.

2 Background: De Borda method with criteria’s weighting

The encyclopedia Britannica (2012) records that De Borda method was presented by Jean-Charles De Borda in 1781, in France to be applied in committees composed of more than one individual (multidecisor problem). As described in McLean (1990) and in Barba-Romero et Pomerol (1997), the central idea of this method is to establish a combination of "individual" ranking established by each one of the decision-makers and global ranking. The following steps are performed when applying De Borda:

a) Get the evaluators, decision-makers, judges or members of the jury

b) Define the elements or alternatives to be ranked

c) Get from each evaluator its perception in terms of the alternatives’ performance

d) Associate a "ranking score" for every alternative, considering the evaluations gotten in the previous step

e) For each alternative, sum the score rankings and obtain overall ranking score

f) Obtain the final ranking of the alternatives.

Barba-Romero & Pomerol (1997) emphasized that the De Borda method should also be applied to situations involving multiple criteria evaluation. In this case, it is just necessary to replace evaluators by decision criteria.

It is also quite simple to adopt a variation of the method in order to take into account the weighting of criteria. To do this, once knowing the weight of each criterion, multiply it by the performance of the alternatives as the usual weight sum approach. The algorithm for De Borda with criteria’s weighting carries out the following steps:

a) Define the elements or alternatives to be ranked

b) Selection of the criteria set

c) Evaluate alternatives under each criterion

d) Based on the evaluations gotten in the previous step, associate a ranking score for every alternative, in each criterion

e) Assign weights to each criterion

f) For each alternative, obtain the weighted sum of the ranking scores, obtaining a global ranking score

g) Get the final ranking of the alternatives, on the basis of the overall ranking numbers.

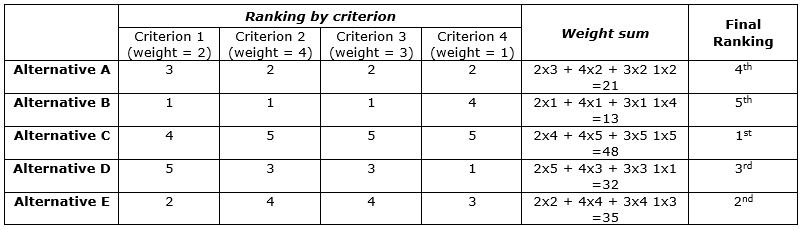
As an example, assume the evaluation of 5 alternatives data and also the criteria weights shown in columns 2, 3, 4 and 5 of Table 1. The last column shows the final ranking one should obtain applying the algorithm above to these data.

Table 1. Ranking of alternatives taking into account the weighting of criteria.

Table 1

3 Background on AHP method

The AHP (Analytic Hierarchy Process) was proposed by Saaty (1977) for the treatment of problems of choice (P. ). If a brief description of AHP core aspects is followed, details from this method can be found in Saaty (1977), Saaty (1980), Vargas (1990), Saaty (1994). This method is based on three principles of analytical thinking:

Construction of hierarchies: in which the problem is deployed in hierarchical levels in the form of a tree or hierarchy of criteria, aiming at a better understanding and assessment of the problem;
Prioritization: which performs the calculation of priorities, taking into account the perception in terms of the relative preference of objects and, also, pairwise comparisons regarding the importance of criteria;
Logical consistency: in the AHP it is possible to calculate de degree of consistency or coherence of the judgments issued by the evaluators.
The following steps are performed in the construction and use of a prioritization model based on AHP:

a) Define the problem and of the general constraints that delimited the space of viable solutions

b) Specify the primary focus or general objective of the modeling

c) Determine a set of feasible alternatives

d) Define the hierarchy of criteria

e) Select a set of evaluators that will convey their pairwise judgments about:

e.1) Criteria importance

e.2) Alternatives’ preferences

f) Determine relative importance of the criteria

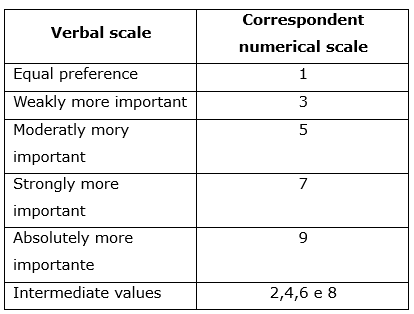
f.1) Collect pairwise judgments: in this step evaluators communicate their perception about relative importance of each criterion, based on the scale shown in Table 2;

f.2) Calculate the relative importance of the criteria, on a sharing base;

f.3) Compute the reason of the consistency ratio (RC) of the pairwise comparisons;

g) Determine the relative preference of the alternatives

g.1) Collect pairwise judgments: in this step evaluators communicate their perception about relative preference of each alternative, under each criterion and using the scale shown in Table 2

g.2) Calculate the relative preference of each alternative, on a sharing basis

g.3) Compute the consistency ratio (RC) of the pairwise comparisons;

h) Calculate the overall priority of each alternative regarding the main focus. To do this: build a weight sum that should combine the alternatives preference defined in step g, with the criteria weights calculated in step f.

i) Construct an alternatives’ ranking, based on the results obtained in step h.

j) Choose the top one alternative in the ranking.

Table 2. Saaty’s Scale for pairwise comparisons

Table 2

4 Proposal: a hybrid AHP-De Borda ranking model

As can be seen in section 2, the De Borda method was developed to achieve the ranking of alternatives (p. γ problem) and in its step (c), in terms of the needs of the assignment weights as input data, which fits a sharing problem (p. σ). Usually the distribution of weights occurs intuitively:

Assuming criteria’s weight as is an input information, obtained prior to modeling the problem for a multi-criteria method.
Using a voting system based on Likert-type scales to assign subjective weights
Adopting the apportionment of weights, usually making the sum of the weights equal to 100
Using the weights swing technique proposed in Edwards (1977) and;
Applying techniques of consensus (Delphi method or Brainstorming, among others) – generally, in the employment of these techniques, the Likert-based scales or assessment techniques of weights is adopted as a backdrop for obtaining the weights of the criteria.

On the other hand, the AHP approaches the criteria’s weights assignment – see step (f) of section 3. The adoption of AHP for generating weights was already validated in Costa (1994), who adopted AHP for generating the weights of a multiobjective function in the context of mathematical programming. Later, Costa et Corrêa (2010) explored this AHP feature for generating weights for the problem of classifying the degree of satisfaction on post-occupancy of habitations. Méxas et al. (2012) explore the use of AHP for obtaining weights in processes of prioritization of criteria for the selection of ERP systems.

The proposal here is to integrate the step (f) of AHP (see section 3) into the step (c) of De Borda (see section 2), resulting in a ranking method, which is structured in the following steps:

a) Define the elements or alternatives to be ranked

b) Select a set of criteria set

c) Evaluate alternatives under each criterion

d) Based on the evaluations gotten in the previous step, associate a ranking score for every alternative in each criterion

e) Assign weights to each of the criteria

e.1) Collect pairwise judgments about the relative importance of each criterion, using the scale shown in Table 2

e.2) Calculate the relative importance of each criterion, on a sharing basis

e.3) Calculate the consistency ratio (RC) of the pairwise comparisons

f) For each alternative, obtain the weighted sum of the ranking scores, obtaining a global ranking score

g) Get the final ranking of the alternatives, on the basis of the overall ranking numbers.

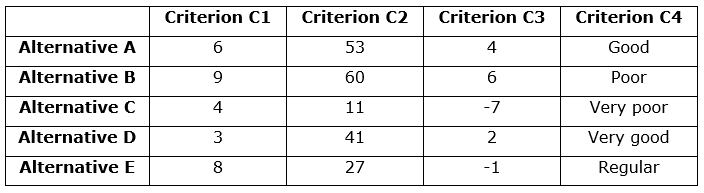
It follows an example, in order to describe the proposal. Consider, without loss of generality, that in a given decision situation, the step (c) led to the data reported in Table 3. In this situation, five alternatives were evaluated under four criteria. Note that different scales, including a verbal one in Criterion 4, were adopted for each criterion.

Table 3. Performance of alternatives under each criterion

Table 3

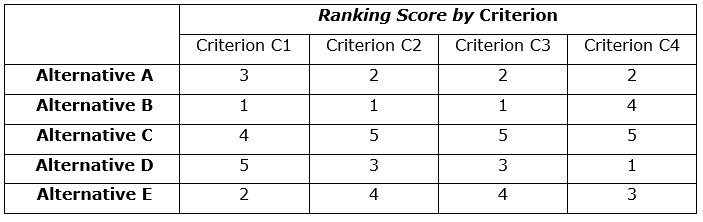
Performing the step (d), it results in the ranking scores assigned to each alternative, as one can see in columns 2, 3, 4 and 5 of Table 4.

Table 4. Ranking scores assigned to each alternative.

Table 4

Consider that, in the step (f.1), the following pairwise comparisons were performed by the evaluators regarding the importance of the criteria: criterion C1 was considered moderately more important than criteria C2 and C3; and, with equal importance to criterion C4. On the other hand C2 and C3 were considered as being equally important, while C4 was considered moderately more important than C2 and C3. Table 5.a shows the judgment matrix that records these judgments, while Table 5.b shows the normalized values of these judgments and the criteria’s weights that come from AHP’s algorithm of prioritization.

Table 5.a. Pairwise comparison of criteria importance

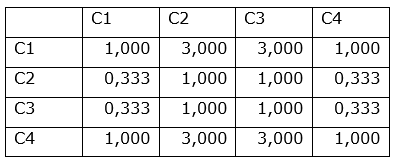
Table 5.a

Table 5.b. Normalized matrix and criteria weights

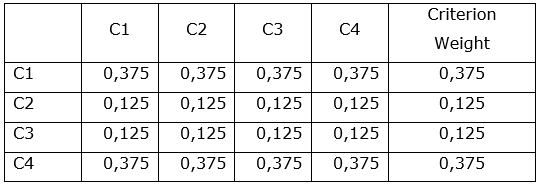
Table 5.b

The Consistency Ratio (RC) of the judgments in Table 5.a was RC= 0.00 and was determined by carrying out the algorithm reported in Saaty (1980). This value denotes that these judgments were consistent.

The ranking scores shown in Table 4 were weighted by the criteria weights that appear in Table 5.b, resulting in a global score ranking shown in the last column of Table 6. Finally, the step (g) was performed, resulting in the ranking that appears in the last column of Table 6.

Table 6. Ranking of the alternatives

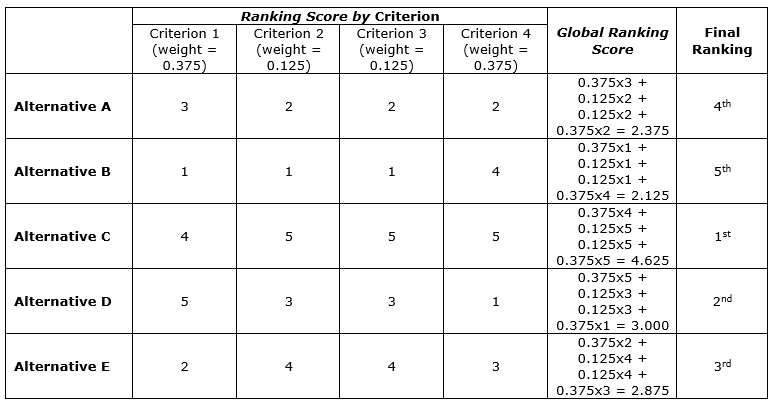
Table 6

Conclusion

This paper described the AHP-De Borda multicriteria method, in which the decision problem of ranking was structured on two levels:

In the first level, the assignment of weights to the criteria is performed, which fits multi-criteria sharing p. σ problem. At this level, the problem was approached by the AHP method, which, in its essence, solves problems of sharing, with the possibility of evaluating the degree of consistency of pairwise evaluations through the calculus of the consistency ratio (RC).
At the second level, a ranking sorting problem (p. y) appears. In this context, the problem is approach by the weight De Borda method, which, in its essence, was proposed to build a ranking of alternatives. In this second level, the distribution of weights, obtained from AHP, was used as input data for the weighted ranking method.

This hybrid approach contributes to knowledge by proposing a better structuring of the problem regarding the integration of an approach that natively supports the assignment of weights (AHP) to another devoted to the ordering of objects (De Borda). This knowledge can assist and support in the modeling of multicriteria ranking problems with assigning weights to the criteria systematically and closer to reality.

AHP and De Borda are based on principles from different multicriteria Decision Schools: AHP is classified into the American School; De Borda is recognized as a French method. Despite this fact, this paper shows that, there, it is possible to use both, in a complementary way by segmenting the problem into two ones and applying each technique for the specific piece of the problem.

It is observed that, despite the fact that AHP has the limitation of joint comparisons of up to a maximum of nine elements, it does not imply a limitation to the number of variables to be considered in the modeling. In such case, it becomes sufficient to structure the variables in a tree or hierarchy of criteria and sub-criteria. As an example, if a problem involves the ranking of alternatives under a set of 15 variables, these may be grouped, for example, in 5 criteria, each with three sub-criteria.

As future works it is suggested to apply the proposal to a set of cases in order to explore and better define its limitations.

References

Arrow, K. J. (1951). Social choice and individual values. New York, London: Wiley, Chapman & Hall.

Barba-Romero, S., Pomerol, J. C. (1997). Decisiones multicritério: Fundamentos teóricos y utilizacion prática. Madrid: Universidad de Alcalá.

Changkong, Y., Haimes, Y. (1983). Multiobjective Decision Making. Amsterdam: Ed. North Holland.

Costa, H. G. (2016). Graphical interpretation of outranking principles: avoiding misinterpretation results from ELECTRE I. Journal of Modelling in Management, Vol. 11, No. 1. doi: doi:10.1108/JM2-08-2013-0037

Costa, J. F. S. (2011). A Genetic Algorithm to Obtain Consistency in Analytic Hierarchy Process. Brazilian Journal of Operations & Production Management, Vol. 8, No. 2, pp. 53-64.

Figueira, J., Greco, S., & Ehrgott, M. (2005). Multiple criteria decision analysis: state of the art surveys. New York, USA: Springer.

Figueira, J. R., Almeida-Dias, J., Matias, S., Roy, B., Carvalho, M. J., & Plancha, C. E. (2011). Electre Tri-C, a multiple criteria decision aiding sorting model applied to assisted reproduction. International Journal of Medical Informatics, Vol. 80, No. 4, pp. 262-273. doi: 10.1016/j.ijmedinf.2010.12.001

Fishburn, P. C. (1964). Decision and value theory. New York: Wiley.

Gomes, C. F. S., Gomes, L. F. A. M., Maranhão, F. J. C. (2010). Decision analysis for the exploration of gas reserves: Merging TODIM and THOR. Pesquisa Operacional, Vol. 30, No. 3, pp. 601-617. doi: 10.1016/j.mcm.2009.02.013

McLean, I. (1990). The Borda and Condorcet principles : three medieval applications, . Soc. Choice Welf, Vol. 7, No. 2, pp. 99-108.

Nepomuceno, L. D. O., & Costa, H. G. (2015). Analyzing perceptions about the influence of a master course over the professional skills of its alumni: A multicriteria approach. Pesquisa Operacional, Vol. 35, No. 1, pp. 187-211. doi: 10.1590/0101-7438.2015.035.01.0187

Pereira, V., & Costa, H. G. (2015). Nonlinear programming applied to the reduction of inconsistency in the AHP method. Annals of Operations Research, Vol. 229, No. 1, pp. 635-655. doi: 10.1007/s10479-014-1750-z

Roy, B., & Boyssou, D. (1985). Mèthodologie Multicritère d’Àide à la Dècision. Paris Ed. Economica.

Saaty, T. L. (1977). A scaling method for priorities in hierarchical structures. Journal of Mathematical Psychology, Vol. 15, No. 3, pp. 234-281.

Saaty, T. L. (1980). The Analytic Hierarquic Process (W. d. S. e. Silva, Trans.). Pittsburg: RWS Publications.

Saaty, T. L. (1994). Fundamentals of decision making and prority theory with the analytic hierarchy process (1st ed.). Pittsburgh, PA: RWS Publications.

Sant'Anna, A. P., Costa, H. G., & Pereira, V. (2015). CPP-TRI: A sorting method based on the probabilistic composition of preferences. International Journal of Information and Decision Sciences, Vol. 7, No. 3, pp. 193-212. doi: 10.1504/ijids.2015.071372

Vargas, L. G. (1990). An overview of the Analytic Hierarchy Process and its applications. European Journal of Operational Research, Vol. 28, pp. 2-8.

Zeleny, M. (1982). Multiple Criteria Decision Making. New York: McGraw-Hill.